Method: 2nd Derivative Test

The 2 ^nd Derivative Test method is almost identical to the 1 ^st Derivative Test method. Basically, take the 1 ^st Derivative on every step of the 1 ^st Derivative Test, and instead use the 2 ^nd Derivative. The meanings are different, but the steps are the same.

Step 1: Find the 2 ^nd Derivative, $f\prime \prime \left(x\right)$.

Step 2: Find the location of the possible inflection pointswhere $f\prime \prime \left(x\right)=0$ or $f\prime \prime \left(x\right)=\mathrm{ }\mathit{Does}\mathrm{ }\mathit{Not}\mathrm{ }\mathit{Exist}\mathrm{ }\left(\mathit{DNE}\right)$

Inflection points can possibly occur where the 2 ^nd Derivative equals zero, $f\prime \prime \left(x\right)=0$, or does not exist, $f\prime \prime \left(x\right)=\mathrm{ }\mathit{Does}\mathrm{ }\mathit{Not}\mathrm{ }\mathit{Exist}\mathrm{ }\left(\mathit{DNE}\right)$.

–           To look for inflection points where $f\prime \prime \left(x\right)=0$, take your second derivative, $f\prime \prime \left(x\right)$, and set it equal to zero and solve for x .

–           To look for inflection points where$f\prime \prime \left(x\right)= \mathit{Does\; Not\; Exist }\left(\mathit{DNE}\right)$, you want to look for places that would “break math”. These “breaking math” locations are most often going to occur when you have a fraction , and you have to consider when you would get division by zero. Division by zero is an example of “breaking math”, you are not allowed to divide by zero. Whatever x-value would cause that to happen would “break math”.

To help yourself identify fractions in your second derivative, look for negative exponents . If you see a negative exponent you will want to apply your Laws of Exponents rewrite in order to turn all your negative exponents positive . I always say negative exponents are great for doing calculus they suck for doing algebra .

–           Other examples of “breaking math” would be square roots of negative numbers , logarithms of negative numbers , or x-values that were not in the domain of your original equation, $f\left(x\right)$.

Step 3: Do the 2 ^nd Derivative Test (number line game)

–           Draw a number line.

If you are provided an x-interval , [ a , b ], make those endpoints the ends of your number line.

–           Mark all of your possible inflection points on the number line.

–           Choose test values on either side (left and right) of your possible inflection points , and mark them on the number line.

–           Do the actual 2 ^nd Derivative Test.

Plug your test values into your 2 ^nd Derivative, $f\prime \prime \left(x\right)$. Remember math people are not creative namers. It is called the 2 ^nd Derivative Test because you are testing everything in the 2 ^nd Derivative, $f\prime \prime \left(x\right)$.

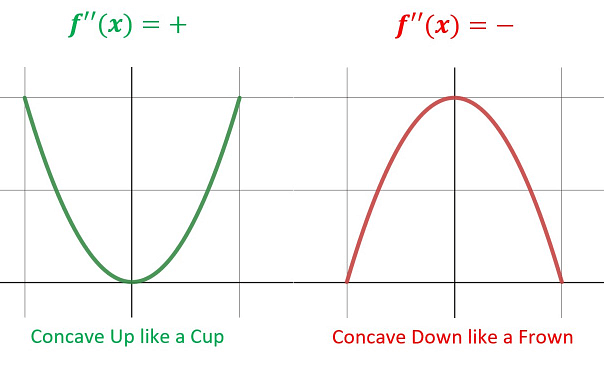
–           Mark the results either positive (concaveup) or negative (concave down) on your number line.

Include a drawing of the concavity that goes with that behavior.

Step 4: Draw Conclusions

Now that you have completed the 2 ^nd Derivative Test, you read that 2 ^nd Derivative information from the number line to answer actual question .

–           If you have been asked to determine the intervals, x-intervals , where the original equation, $f\left(x\right)$, is concaveup or concave down, they will generally want to see that answer in what is called interval notation (how convenient). They will generally want to see that answer in what is called interval notation (how convenient). Interval notation looks like ( a , b ) or [ a , b ]or some combo ( a , b ]. Where parenthesis, (   ), mean the endpoint is not included , and brackets, [   ], mean the endpoint is included . You will not want to include the endpoints at your endpoints the function is not concave up or concave down. When you need to connect multiple intervals for a solution you will need to use a union symbol , $\left(a,b\right)\mathit{\cup }\left(c,d\right)$.

–           If you have been asked to identify inflection points you will need to make sure the point fits both requirements of an inflection point .

1)      $f\prime \prime \left(x\right)=0$ or $f^{\prime \prime }\left(x\right)=\mathit{DoesNotExist}\left(\mathit{DNE}\right)$

2)      The function must change concavity at that x-value .

–           If your x-value does meet both of those requirements, then you will need to plug that x-value back into the original equation, $f\left(x\right)$, to find the y-value that goes with it. Remember at this stage in the process you only have the x-value of your inflection point , and that the y-value is required to create the actual ( x , y ) of the inflection point .