Linearization = Tangent Line Approximation = Local Linear Approximation

Unit 4: Application of Derivatives Linearization = Tangent Line Approximation = Local Linear Approximation

Guess what? All of those terms, linearization, tangent line approximation, and local linear approximation, are talking about the exact same thing.

And guess what? They are all asking you to find the equation of the tangent line. Yeah, that equation of the tangent line from your previous work. Got to love math people.

Meaning: Linearization = Tangent Line Approximation = Local Linear Approximation

Essentially what is happening is that you are using the equation of the tangent line to approximate another more complex equation, $f (x)$ , at a single point, $(x_{1}, y_{1})$ , the tangent point.

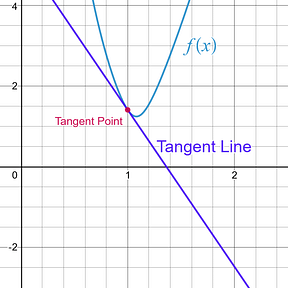
When you look at the image above, you can see that the tangent line and the actual equation, $f (x)$ , visually start looking like the same graph the closer the two graphs get to the tangent point. For x-values that are very, very, very close to the tangent point, the tangent line can be used to approximate y-values for the actual equation, $f (x)$ .

Note :

What you are creating here is an easy-to-use equation that you can use to approximate a more complicated equation.

I find it helpful to understand how people historically used this process when trying to wrap my head around what is happening.

Let’s say you wanted to know the value of $\sqrt{4.14}$ . Well, today you would just pick up your phone, type it in, and get the answer accurate to as many decimal places as you would like. However, 150 years ago the answer to that math problem was not so easy to find. You either had to work it out by hand, which could take a while depending on the problem, or, if you were lucky, you would have a book filled with tables of precalculated values for square roots on your shelf, or maybe you had a friend the next town over who had that book.

Now let’s say you needed to calculate a value for an equation like $f (x) = \sqrt{{5 x}^{4} + {7 x}^{- 3} - 10 x}$ ; you can see how the more complicated the equation, the more complicated it would to find that value.

A linear equation, y = mx+b , on the other hand, is always an easy-to-use equation for plugging in x-values and getting out answers, y-values .

Since the tangent line is extremely close to the actual equation, $f (x)$ , at the tangent point, they said why not just use the tangent lineequation to get the value you need? In many situations it would be good enough to use in place of the actual value, and you don’t need to travel to the next town to look it up.