Example 1: Mechanical

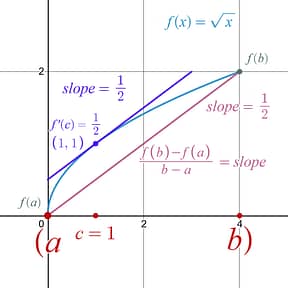
The Mean Value Theorem guarantees the existence of a special point on the graph of $f\left(x\right)=\sqrt{x}$ on the x-interval [0,4]. What are the coordinates of this point?

Step 1: Assure that the requirements of the Mean Value Theorem are met by your situation or equation.

These are just statements that you must make, but you don’t need to actually prove those statements. This is one of those unique moments in math where if you state it and it is true, they give you the credit and believe you.

The given function $f\left(x\right)=\sqrt{x}$ is known to be:

i)                     continuous on the closed interval [0,4]

ii)                   differentiable on the open interval (0,4)

Step 2: Find the averagerate of change, slope ,between the two x-value endpoints, [ a , b ] of your function.

$\mathit{average }\mathit{rate\; of\; change}=\frac{f\left(b\right)–f\left(a\right)}{b–a}$

[ a , b ]= [0,4]

$f\left(x\right)=\sqrt{x}$

$f\left(b\right)=f\left(4\right)=\sqrt{4}=2$

$f\left(a\right)=f\left(0\right)=\sqrt{0}=0$

$\frac{f\left(b\right)–f\left(a\right)}{b–a}=\frac{f\left(4\right)–f\left(0\right)}{4–0}=\frac{2–0}{4–0}=\frac{2}{4}=\frac{1}{2}$

Step 3: Find the derivative of your equation, $f\prime \left(x\right)$.

$f\left(x\right)=\sqrt{x}$

$f\left(x\right)=x^{\frac{1}{2}}$

$f\prime \left(x\right)=\frac{1}{2}{x}^{–\frac{1}{2}}$

Step 4: Set your derivative, $f\prime \left(x\right)$, equal to your $\mathit{average }\mathit{rate\; of\; change}=\frac{f\left(b\right)–f\left(a\right)}{b–a}$, then solve that algebra problem for x .

Algebra Moves:

1)      Multiply both sides by 2 to isolate the x .

2)      Raise both sides to the -2 power to get x to the first power. Remember x is really raised to the 1 ^st power, we just never really write that 1.

$\frac{f\left(b\right)–f\left(a\right)}{b–a}=f\prime \left(x\right)$

$\frac{1}{2}=\frac{1}{2}{x}^{–\frac{1}{2}}$

1)      $2\bullet \frac{1}{2}=2\bullet \frac{1}{2}{x}^{–\frac{1}{2}}$

$1=x^{–\frac{1}{2}}$

2)       ${\left(1\right)}^{–2}={\left(x^{–\frac{1}{2}}\right)}^{–2}$

$1=x^1=x$

x = 1 is in the open interval (0,4).

Final Results:

At this point in your process, you have only found the c-value , x = 1 , that the MVT guaranteed would exist on the open interval (0,4). In some problems that is the final answer they only want the x-value . This problem takes it one step further an says it wants the “coordinates” of the point. If you are asked for the coordinates or a point, that means you need to provide a full ( x , y ) coordinate not just the x-value.

To reach the final result you would need to plug x=1 back into the original equation , $f\left(x\right)=\sqrt{x}$, to get the full coordinate.

$f\left(1\right)=\sqrt{1}=1$

(1,1) is the coordinate of the special point guaranteed by the MVT.

Here is what this looks like in terms of a graph.