Method: 1st Derivative Test

Step 1: Find the 1 ^st Derivative, $f^{\prime }\left(x\right)$.

Step 2: Find the critical values of the equation.

Critical values are the places where the derivative equals zero, $f^{\prime }\left(x\right)=0$, or does not exist , $f^{\prime }\left(x\right)=\mathit{DNE}$.

• To look for critical values where $f^{\prime }\left(x\right)=0$, take your derivative, $f\prime \left(x\right)$, and set it equal to zero and solve for x.
• To look for critical values where$f^{\prime }\left(x\right)= \mathit{Does\; Not\; Exist }\left(\mathit{DNE}\right)$, you want to look for places that would “break math”. These “breaking math” locations are most often going to occur when you have a fraction , and you have to consider when you would get division by zero. Division by zero is an example of “breaking math”, you are not allowed to divide by zero. Whatever x-value would cause that to happen would “break math”.

To help yourself identify fractions in your derivative, look for negative exponents . If you see a negative exponent you will want to apply your Laws of Exponents rewrite in order to turn all your negative exponents positive . I always say negative exponents are great for doing calculus they suck for doing algebra .

• Other examples of “breaking math” would be square roots of negative numbers , logarithms of negative numbers , or x-values that were not in the domain of your original equation, $f\left(x\right)$.
• If you have a closed interval, [ a , b ] , then the endpoints of that interval would also be places where, $f^{\prime }\left(x\right)=\mathit{DNE}$, and so you would want to consider them as critical values as well.

Most people remember the first option, the derivative equals zero, but most people forget about the second option, where the derivative does not exist .

Also, critical values are the places where our original equation, $f\left(x\right)$, has either a horizontal tangent lines (zero slope), or is not differentiable (so not smooth or not continuous). These are the possible locations of maxes and mins; they are not always a max or a min.

Step 3: Do the actual 1 ^st Derivative Test (number line game).

This is the point in the method where you actually do the 1 ^st Derivative Test.

• Draw a number line.
• Mark all critical values on the number line.

Remember that the endpoints of an x-interval are also critical values and should be marked as the endpoints of your number line.

• Choose test values on either side ( left and right ) of all your critical values , and mark them on the number line.

If you have endpoints on your number line due to a closed x-interval , you do not need to mark test values outside the closed x-interval .

• Do the actual 1 ^st Derivative Test.

Plug your test values into your 1 ^st Derivative, $f\prime \left(x\right)$. Remember math people are not creative namers. It is called the 1 ^st Derivative Test because you are testing everything in the 1 ^st Derivative, $f\prime \left(x\right)$.

• Mark the results of the 1 ^st Derivative Test for each of your intervals as either positive (increasing) or negative (decreasing) on your number line.

Including the drawing of the directional arrow that goes with that behavior. Believe me a simple thing like drawing your directional arrows will really help you see what is happening. This gets back to our derivative triangle.

 

When doing a 1 ^st Derivative Test, we don’t care about the actual value of the derivative only if it is positive or negative.

Step 4: Draw Conclusions

Now that you have completed the 1 ^st Derivative Test, you read that 1 ^st Derivative information from the number line to answer actual question .

• If you are being asked to find the local max or min, you want to determine those locations based upon the shape of your directional arrows, or the changing signs of your derivative.

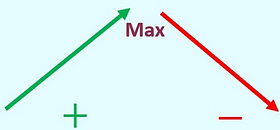
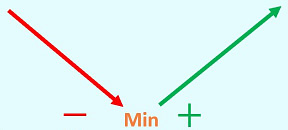
If your critical values do not have either of these shapes, that is fine, it means that it is neither a max or min, and was only a critical value . This is why you perform the 1 ^st Derivative Test; you must prove that your critical value has the behavior of a max or min.

• If you were being asked to find the local max or min, remember that all you have only found at this point in the process is the x-value of that max or min. You know when the max or min occurs. You have not found what the actual max or min is, which is the y-value .

To find the actual max or min y-value , you will need to plug your critical value , x-value , back into the original equation, $f\left(x\right)$. The max or min is a point, ( x , y ) , on the original equation, $f\left(x\right)$.

• If you have been asked to determine the intervals, x-intervals , where the function, $f\left(x\right)$, is increasing or decreasing, then you will read this data directly from your 1 ^st Derivative Test number line .
  • Intervals on your 1 ^st Derivative Test number line where the derivative, $f\prime \left(x\right)$, value is positive, where you have an arrow pointing up are the increasing intervals .
  • Intervals on your 1 ^st Derivative Test number line where the derivative, $f\prime \left(x\right)$, value is negative, where you have an arrow pointing down are the decreasing intervals .

They will generally want to see that answer in what is called interval notation (how convenient). Interval notation looks like ( a , b ) or [ a , b ]or some combo ( a , b ]. Where parenthesis, (   ), mean the endpoint is not included , and brackets, [   ], mean the endpoint is included . You will usually not want to include the endpoints of your intervals because the endpoints will be your critical values , and at your critical values the function is not increasing or decreasing. When you need to connect multiple intervals for a solution you will need to use a union symbol , $\left(a,b\right)\mathit{\cup }\left(c,d\right)$.