Identifier: 1st Derivative Test
There are two main types of problems that you will want to apply the 1 st Derivative Test to; determining local extrema or determining the intervals where your original function, , is increasing or decreasing.
i) Local Extrema
This is another great example of math people now just picking one name and sticking with it. Depending on your instructor you will see these terms being used: Local Extrema meaning Local Max’sand Local Min’s or Relative Extrema meaning Relative Max’s and Relative Min’s. You will want to prepare yourself to recognize both sets terms and be able to mentally use them interchangeably.
If you see terms like maximize, minimize, largest, smallest, and other similar wording meaning max or min, this is cluing you in that you need to run a 1 st Derivative Test.
Meaning: Local Extrema or Relative Extrema
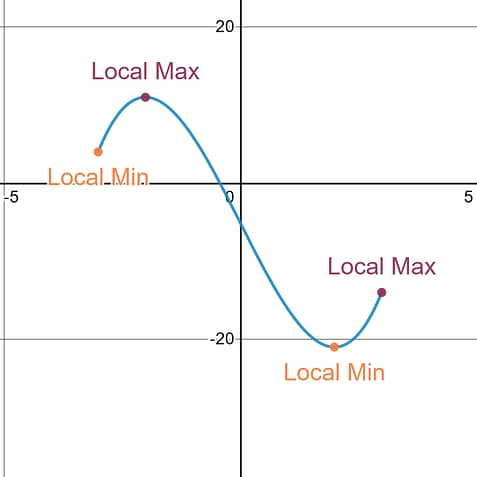
A local or relative max is the largest y-value in its little neighborhood of a graph.
A local or relative min is the smallest y-value in its little neighborhood of a graph.
Note:
Most people remember to look for Local Min’s and Local Max’s and the peaks and valleys of a graph.
Most people forget to look for Local Min’s and Local Max’s at the endpoints of an interval, [a,b].
If you look at the graph above you will see the left-endpoint is marked as a Local Min. This is because compared to all the other y-values very close to it (in its neighborhood), it is the smallest y-value . It is a Local Min.
If you look at the right-endpoint on the graph it is marked as a Local Max. This is because compared to all other y-values very close to it (in its neighborhood), it is the largest y-value . It is a Local Max.
ii) Intervals of Increasing and Decreasing
If you are asked to determine the intervals where a function is increasing or decreasing, then you will definitely need to run a 1 st Derivative Test. This is another application of the derivative triangle we keep talking about.
