Mean Value Theorem

Definition: Mean Value Theorem (MVT)

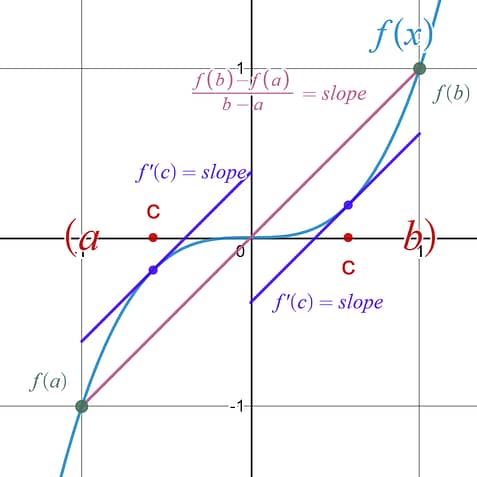
If the function $f\left(x\right)$ is continuous on the closed interval [ a , b ] and differentiable on the open interval ( a , b ), then there is a number c such that a < c < b and $f\prime \left(c\right)=\frac{f\left(b\right)–f\left(a\right)}{b–a}$.

Everyday Language:

Essentially what the Mean Value Theorem is saying is if you have an equation, $f\left(x\right)$, that is continuous (you can’t lift your pencil) and differentiable (there is a derivative value everywhere), then you are guaranteed this cool thing happens.

The cool thing that happens is that you are guaranteed that you can find an x-value , c , that is inside your x-interval , ( a , b ), so that the slope between those two x-interval endpoints, [ a , b ], $\frac{f\left(b\right)–f\left(a\right)}{b–a}=\mathit{average }\mathit{rate\; of\; change}$,  will be equal to the slope of the tangent line at that x-value , c , $f\prime \left(c\right)=\mathit{slope }\mathit{of }\mathit{tangen}t\mathit{ line}$.

$f\prime \left(c\right)=\frac{f\left(b\right)–f\left(a\right)}{b–a}$

$\mathit{slope }\mathit{of }\mathit{tangent\; line}=\mathit{average }\mathit{rate\; of\; change}$

In the example graph above you can see that there are actually two c-values , x-values , in the interval ( a , b ), such that the slope at those points would be equal to the slope between the two endpoints. The MVT only guarantees you one x-value , but you could absolutely have multiple x-values that make the statement true.