Finding the Equation of the Tangent Line
One of the more popular applications of a derivative is to actually find the equation of the tangent linethat we keep referring to.
The reason this is such a common question, is because the information you use to create the equation of any line, a point, , and a slope, m , are always going to be something you are always able to easily find. Once you have a point, , and a slope, m , you can then create the equation of any line using the point–slope form for a line . The name says it all you need is a point, , and a slope, m , then you can create the equation of any line .
Meaning: Tangent Line
Tangent line means a line ( linear equation ) that touches your actual equation, , at just one point, , one instance. That tangent point is the intersection of your tangent line and the original equation, .
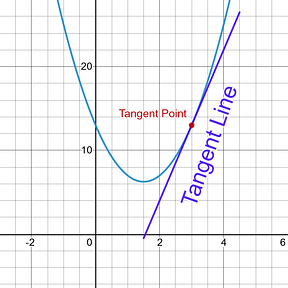
Note :
– This is not tangent like the sine , cosine , tangent that you learned in your trig class. They are not related to each other at all.
Definition: Point – slope form of a line.
Note :
– I know that this version of the Point–Slope Form of a Line is probably slightly different than the one in your textbook or the one your instructor is using. I prefer this version because it takes one step of algebra out of the process by moving the to the right of the equals sign to start with. I guarantee you that it is the exact same thing, and that there is absolutely nothing wrong with using this form. You will get all the points you deserve on any exam if you use this form, and it is by far the better way to memorize the formula.
– If you would like to stick with the more common version, and do the algebra on your own, then here is a more standard point–slope form for a line .
