2nd Derivative Test Option 2: Finding Local Max and Local Min
There is a way you can use the 2 nd Derivative to determine if your critical values are local max’s or min’s. I generally stay away from this method unless they absolutely make me do it. My philosophy is, if I can get it all from the 1 st Derivative, then why would I want to find a 2 nd Derivative? Finding that extra derivative just gives me one more step where I could mess something up. Additionally, there is the possibility that the 2 nd DerivativeTest for max and min could just flat out fail, and you would not be able to draw any conclusions. Yep, that can happen.
Some people find they don’t mind taking a 2 nd Derivative, and find this method to be their preferred way of always determining the local extrema when asked. This method is just as legit on the AP Calculus Exam as a 1 st Derivative Test for finding local max and min. If you find that you like this method better, then please keep using it to find all the relative extrema when you are asked.
Concept: 2 nd Derivative Test for Finding Local Max and Local Mins
The 2 nd Derivative Test assumes that you are testing critical values.
From that 2 nd Derivative Test,you have two results possible.
|
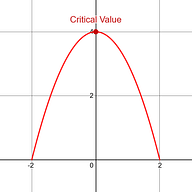
Option 1:
is positive |
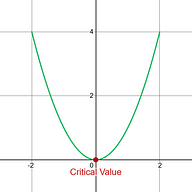
Option 2:
is negative |
|
|
|
|
Meaning : A critical value in concave up section, means you have a local min. |
Meaning : A critical value in concave down section, means you have a local max. |