Example 1: Optimization

You are wanting to fence in a rectangular garden using your house as one side of the garden. You have 32ft of fencing to use, and want to fence in the largest area possible. What are the dimensions of your garden, and what is the area?

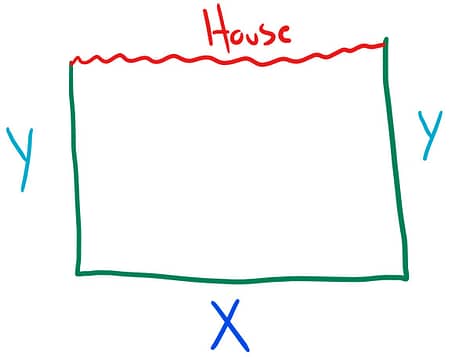
Step 1: Draw a picture of the situation.

In this situation you are trying to fence your rectangular garden, but you don’t need to fence one side of the garden because it is next to your house.

Step 2: Label the picture you drew.

You can label this however you would like, but generally I like to label the horizontal sides as x , and my vertical sides y . But this is all about what makes sense in your brain.

Step 3: Create a constraint equation.

Your constraint will usually be associated to a flat amount, or value given to you in the language of the actual problem.

In this problem we have a flat amount of fencing, 32ft. The fencing is what we would use around the edges of the shape we drew. This means the fencing is a constraint on the perimeter of our shape. The perimeter is the distance around the outside of the shape.

Based on our picture in Step 2, we can see the perimeter here would be $\mathrm{}$$P=2y+x$

Generally, your constraint will be areas, volumes, more common geometry shapes.

Set your constraint equation equal to the constraint, and solve the constraint equation for one of the variables you want to substitute into your optimization equation, and then substitute it into the optimization equation.

Our perimeter is constrained by the 32ft of fencing that we have to use.

This means we need to set our constraint equation equal to 32.

$P=2y+x$

$32=2y+x$

Step 4: Create your optimization equation .

To create the optimization equation , you need to look for the language that describes what exactly you are trying to maximize for minimize .

This problem wants you to find the “ largest area ” for your garden. You need an area equation that works with the shape you just drew, which was a rectangle .

This is why knowing your standard area and volume formulas is so important.

The area of a rectangle formula is A = (base)*(height) or A = (length)*(width)

You then use the variables that you labeled your picture with to get the equation you want to optimize .

$A=x\bullet y$

You will notice that your equation is not talking just one variable so either all x ’s or all y ’s. This means you are going to need a second equation, a constraint equation , to get this equation to talk only one variable .

You now need to solve the constraint equation , from Step 3, to get one of our variables alone on one side of the equals.

Keep in mind that the long game here is that you need to get the equation you actually want to optimize to talk the language of only one of your variables, either x or y , it doesn’t matter.

This setup makes it easier (in my opinion) to solve for x . That is what you could do.

Once you do that, substitute back into your optimization equation , and ideally you now have one equation of one variable . In your situation your one variable is now the y variable .

$A=\mathit{base}\bullet \mathit{height}$

$A=x\bullet y$

Solve constraint equation for one variable:

$32=2y+x$

$32–2y=x$

Plug constraint equation into the optimization equation:

$A=x\bullet y$

$A=\left(32–2y\right)\bullet y$

Step 5: Once your optimization equation is in one variable , you will start either a 1 ^st Derivative Test or Global Extrema Process depending on if you have endpoints on your interval.

In this example you do not have any end points. In the end you have to have an Area, an actual garden. Neither of your sides could ever equal zero. They could be really close, but not actually zero. And technically one side could be extremely long, so there is nothing to keep you from choosing an extremely large value for one of your sides.

Essentially your Domain (inputs) could be $\left(0,\infty \right)$.

Since you do not have endpoints for your domain, you will run a standard 1 ^st Derivative Test. Starting with the area equation we created in Step 4.

Step 1: Find the first derivative.

Step 2: Find the critical values of the equation.

Step 3: Do the 1 ^st Derivative Test ( Number Line Game ).

You must still show that what you have found is actually a max or a min. It is not enough to just trust that your critical value is what you are looking for.

Step 4: Draw Conclusions

In this situation you have the y-value from your labeled picture, but you still need the x-value (the length of the other side), and the actual max area .

$A=\left(32–2y\right)\bullet y$

Step 1: $\mathrm{}$$A=\left(32–2y\right)\bullet y$

Simplify:

$A=32y–2y^2$

Power Rule:

$A\prime =32–4y$

Step 2:

$0=32–4y$

Move the $4y$ to the left side of the equals.

$4y=32$

Divide both sides of the equation by 4 to get y alone.

$y=8=\mathit{Critical\; Value}$

Step 3: Choose a test value on either side of the critical value , and test them in the first derivative,
$A\prime =32–4y$.

Step 4: Draw conclusions.

You know one side of your garden is the critical value , y = 8ft .

You use your equation you solved for x in Step 4, and plug in your y-value to find the x-value .

$32–2y=x$

$32–2\left(8\right)=x$

$16\mathit{ft}=x$

You can also find our Max Area by plugging the critical value , y = 8ft , into your area equation from Step 4.

$A=\left(32–2y\right)\bullet y$

$A=\left(32–2\left(8\right)\right)\bullet \left(8\right)$

$A=128{\mathit{ft}}^2$

Final Result:

Dimensions: $8\mathit{ft}\times 16\mathit{ft}$

Max Area: $A=128{\mathit{ft}}^2$

Final Result:

Dimensions for the garden with maximum area would be 8ft x 16ft .

The actual maximum area of the garden would be 128ft ² .