Method: Curve Sketching

Step 1: Find $f\prime \left(x\right)$and $f\prime \prime \left(x\right)$.

Step 2: Run the First 3-Steps of the 1 ^st Derivative Test for Intervals of Increasing and Decreasing.

Step 3: Run the First 3-Steps of the 2 ^nd Derivative Test for Intervals of Concave Up and Concave Down.

Step 4: Create a combined number line bringing together the data from your 1 ^st Derivative Test number line and your 2 ^nd Derivative Test number line.

• Start by marking all your critical values and inflection points on the number line.
• Then draw dotted lines down from each of the critical values and inflection points.
• Label on the left-hand side of the number line starting at the top with $f\prime \left(x\right)$, then below that $f\prime \prime \left(x\right)$, and then finally below that $f\left(x\right)$ .
• Finally bring your + and – from your 1 ^st Derivative and 2 ^nd Derivative number lines, and label each of the intervals that were created by your dotted lines.

Step 5: Read the shape of the curve based upon your combined number line, and draw it in the $f\left(x\right)$section of your chart.

There are two sides to each concavity shape , an increasing side and a decreasing side. Use the 1 ^st Derivative, $f\prime \left(x\right)$, data to determine if the graph is + = increasing or – = decreasing, and then use the 2 ^nd Derivative, $f\prime \prime \left(x\right)$, data to know if it is + = concave up or – = concave down.

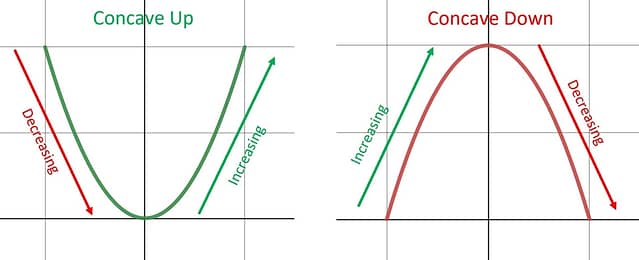
Step 6: Sketch the curve on your graph taking the shapes you drew on your number line, and connecting them at the critical points and inflection points .

• If you were given any specific points, ( x ,y), that had to be on your graph other than the critical points and the inflection points .
• Mark your critical points and inflection points on your graph.

Often times you will need to plug the x-values of your critical values and inflection points back into the original equation, $f\left(x\right)$, to get the y-values that go with those x-values .

• Use your combined number line shapes to connect those dots.

The critical points and inflection points are where your graph is changing behavior.