Example 2: About an axis other than the x-axis

Find the volume of the solid generated by revolving the region bounded by the curves $y=x^2+2,\mathit{ and\; y}=6$ about the line $y=6$.

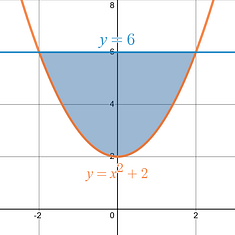
Step 1: Draw out the region that you are being asked to rotate.

In this example you have the curve, $y=x^2+2$, which is a parabola shifted up two units, and you close off the region on the top with the equation $y=6$.

The region that you are being asked to rotate is the shaded region.

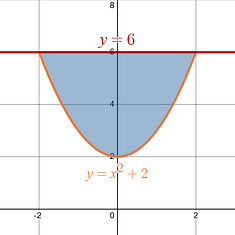
Step 2: Determine the axis you are begin asked to revolve or rotate your region around.

In this problem the language says, “about the line $y=6$”. You are revolving around the horizontal line $y=6$.

Step 3: Determine whether your equation is in terms of x (standard: $y=x^2+3x+\sqrt{x}$) or in terms of y (non-standard: $x=y^2+3y+\sqrt{y}$).

Since you are asked to revolve around the line $y=6$,you know that this is a horizontal axis , and you want to setup your Disk Methodintegral in terms of x .

The given equation , $y=x^2+2$, is ready to use because it is already in terms of x .

Step 4: Determine the bounds of the integral, $\underset{a}{\overset{b}{\int }}$, for each of your enclosed regions.

In this example, since you are not given the points where the region begins and, you will need to find where the two equations intersect each other (i.e., where are the two equations equal to each other).

$x^2+2=6$

Once you set the two equations equal to each other, you solve for x to get your lower bound and upper bound .

You result from the algebra:

$x=–2\mathit{ and }x=2$

The lower bound will be a = -2 , and the upper bound of your integral will be b = 2 .

$x^2+2=6$

$\begin{array}{c}{x}^2+2\\ –2\end{array}=\begin{array}{c}6\\ –2\end{array}$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$x=–2\mathit{ and }x=2$

$\underset{a}{\overset{b}{\int }}=\underset{–2}{\overset{2}{\int }}$

Step 5: Determine your radius equation, $R\left(x\right)$.

I find it very helpful to draw in a couple of example radius lines to show myself what I need to calculate.

In this example you are rotating around the line $y=6$. When drawing out some example radi, start from that axis of rotation , $y=6$,and draw to the other equation, $y=x^2+2$.

You can see that the radius is going to be the distance from the $y=6$to the given equation, $y=x^2+2$. This means you need to find the distance between two equations (remember that while not a very exciting equation that $y=6$ is an equation as well).

The process to find the distance between two equations is to subtract the two equations . You will use the same Top – Bottom process that you applied when finding the Area Between Two Curves. This distance between two equations can always be found using this process.

Your radius equation, R(x) , will be found by the setup:

R(x) = Top – Bottom

The Top equation (the equation that is above the other equation) is going to be $y=6$, and the Bottom equation is going to be $y=x^2+2$.

Remember that when subtracting two equations, the second equation always needs to be in parenthesis. You are subtracting the WHOLE equation.

Plugging the equations into your radius setup, R(x) will be:

R(x) = Top – Bottom

$R\left(x\right)=6–\left(x^2+2\right)$

Simplifying that equation by distributing the negative through the quantity, you get:

$R\left(x\right)=6–x^2–2$

$R\left(x\right)=–x^2+4$

Step 6: Setup up and evaluate your Disk Methodintegral.

Use the results of Step 4 (your bounds ) and Step 5 (your R(x) equation) together using the Disk Methodintegral setup.

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}\pi {\left[R\left(x\right)\right]}^2\mathit{dx}$

The first step in evaluating these Disk Methodintegral will usually be to expand the squared term.

Once you have expanded the squared term, you can factor out (pull to the front) the $\pi$, and then multiply it by the final result of the definite integral at the end of the process.

You will generally be able to handle the definite integral using only the Power Rule.

– Bounds from Step 4 : $\underset{–2}{\overset{2}{\int }}$

– R(x) equation from Step 5 : $R\left(x\right)=–x^2+4$

$\mathit{Volume}=\underset{–2}{\overset{2}{\int }}\pi {\left[–x^2+4 \right]}^2\mathit{dx}$

$\underset{–2}{\overset{2}{\int }}\pi \left(–x^2+4\right)\left(–x^2+4\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4–4x^2–4x^2+16\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4–8x^2+16\right)\mathit{dx}$

$=\pi \bullet \underset{–2}{\overset{2}{\int }}\left(x^4–8x^2+16\right)\mathit{dx}$

$\pi \bullet \left({\frac{x^5}{5}–\frac{8x^3}{3}+16x|}_{–2}^2\right)\mathit{=}$

$\pi \bullet \left(\left[\frac{{\left(2\right)}^5}{5}–\frac{8{\left(2\right)}^3}{3}+16\left(2\right)\right]–\left[\frac{{\left(–2\right)}^5}{5}–\frac{8{\left(–2\right)}^3}{3}+16\left(–2\right)\right]\right)=$

$\pi \bullet \left(\frac{512}{15}\right)=$

$\frac{512}{15}\pi =\mathit{Volume\; of\; Solid}$

Final Result:

The volume of the solid obtained by rotating the region bounded by the curves $y=x^2+2,\mathit{ and }y=6$ about the line $y=6$ is $\frac{512}{15}\pi$.