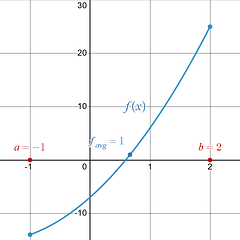
Example 1: Average Value Integral

Determine the average value of $f\left(x\right)={3x}^2+10x–7$ on the interval $\left[[-1,\mathrm{2]}\right]$

Step 1: Setup the Average Valueantiderivative formula.

$f_{\mathit{avg}}=\frac{1}{b–a}\bullet \underset{a}{\overset{b}{\int }}f\left(x\right) \mathit{dx}$

In this example $f\left(x\right)={3x}^2+10x–7$

[ a , b ]=[ -1 , 2 ]

$f_{\mathit{avg}}=\frac{1}{2–(–1)}\bullet \underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}$

$f_{\mathit{avg}}=\frac{1}{3}\bullet \underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}$

Step 2: Evaluate the Definite Integral formula you created in Step 1 .

You would apply the Power Rule with the Top minus Bottom method to get out your definite value for the integral.

You take that definite integral result and multiply it by $\frac{1}{3}$.

$\underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}\mathit{=}{\left.x^3+5x^2–7x\right|}_{x=–1}^{x=2}$

$\mathit{=}\left[{\left(2\right)}^3+5{\left(2\right)}^2–7\left(2\right)\right]–\left[{\left(–1\right)}^3+5{\left(–1\right)}^2–7\left(–1\right)\right]=\mathit{3}$

$\underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}\mathit{=}\mathit{3}$

 
$f_{\mathit{avg}}=\frac{1}{3}\bullet \overline{)\underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}}$  

$f_{\mathit{avg}}=\frac{1}{3}\bullet \overline{)\mathit{3}}$

$f_{\mathit{avg}}=1$

Final Result:

The average y-value for the function $f\left(x\right)={3x}^2+10x–7$ over the x-interval [ -1 , 2 ] is y=1 .