Disk Method

Definition: Volumes of Solids (Rotation): Disk Method

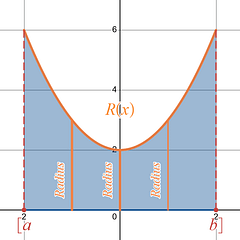
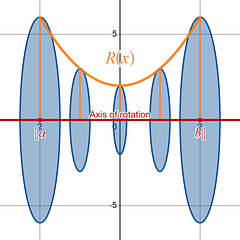
The Disk Method is called that because what you are doing is creating a bunch of little disks or circles (slices of bread) that you add up , accumulate , to create the total volume of your solid (the loaf of bread). The disks are created by using the x-axis , y-axis , or another provided axis as your axis of rotation; from that axis you draw a line up to the curve, creating the radius of your disk . You then rotate that line 360 ^◦ around the given axis . What you have now created is a disc or circle (a slice of bread).

How I like to try and visualize this is to think about holding one end of a crayon down on a piece of paper, and then rotate the crayon 360 ^◦ around the end of the crayon ( axis ) you are holding down. When you lift your crayon up you are left with a circle that has the radius of however long your crayon was.

The Disk Method integration formula for finding the volume of a solid rotated around an axis is

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}\pi {\left[R\left(x\right)\right]}^2\mathit{dx}$

What it means:

Keep in mind that the shape you are creating is a disk or a circle . The general area formula for a circle is $\mathit{Area\; of\; Circle}=\pi r^2$, which is exactly where the form of the Disk Method integration formula comes from.

The equation you are given to rotate around an axis will be what creates the radius of your disk or circle , the $R\left(x\right)$.

The slices of bread are those disks or circles , and the volume of the loaf of bread comes from adding up all the slices, all your disks or circles .

You add up all the disks using your antiderivative, which is an accumulation tool, and the bounds of that antiderivative, [ a , b ], are the length of your x-interval , or the length of your loaf of bread, $\underset{a}{\overset{b}{\int }}$.

$\mathit{Loaf}=\underset{a}{\overset{b}{\int }}\mathit{Slices}\mathit{dx}$