Area Between Two Curves = Region Bounded by Two Curves

Definition: Area Between Two Curves or Region Bounded by Two Curves

Much like the Average Value formula, this is a Definite Integral formula that you setup when requested, and then run your standard Definite Integral process on your setup.

$\underset{a}{\overset{b}{\int }}\mathit{Top}–\left(\mathit{Bottom}\right)\mathit{dx}=\mathit{Area\; Betwen }2\mathit{ Curves}$

What it means:

Essentially what is happening is that you are taking the entire area under the Top equation and subtracting out of that space all the area under the Bottom equation, which leaves you with only the area that is between the two curves or bound by those two curves.

When I use the term Top, I am referring to the equation that is above the other equation visually. When I use the term Bottom,I am referring to the equation that is below the other equation.

Depending on your specific problem you could have the positions of your graphs stay the same over the given interval, [ a , b ], or the positions could reverse (change which one is on top and which one is on bottom). This would mean you would need to do multiple Area Between Two Curve setups to account for those changes in top and bottom.

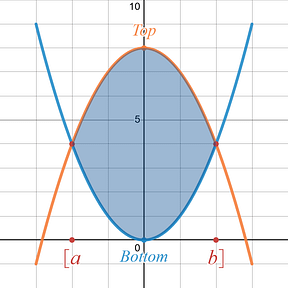
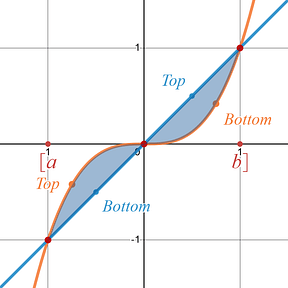
Note: The answer to these problems will ALWAYS BE POSITIVE. You cannot have negative area between two curves.