Accumulation Tool
Definite integrals when applied to “real world” situations are often used to calculate an accumulated amount of something occurring at a specific rate, i.e., derivative or differential equation . What you are accumulating is the units of what is “on top” in the dy position of your differential notation, rate of change, or derivative. If you are given a rate of change in the units meters per second , , then the definite integral would provide you with an accumulated amount of meters , the units “on top”.
One extremely important distinction you will always need to be aware of is whether you are being asked to find the Net amount or the Total amount. This is the same distinction you needed to be aware of when doing your standard definite integral processes. They could either ask you for the Net area or the Total area.
|
Total Accumulation |
|
|
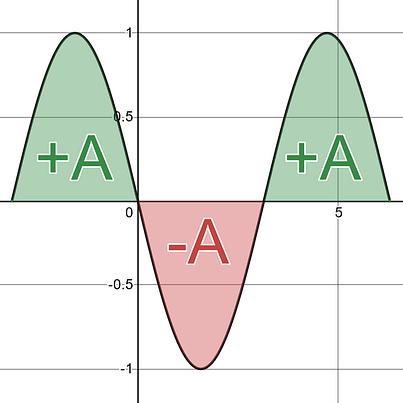
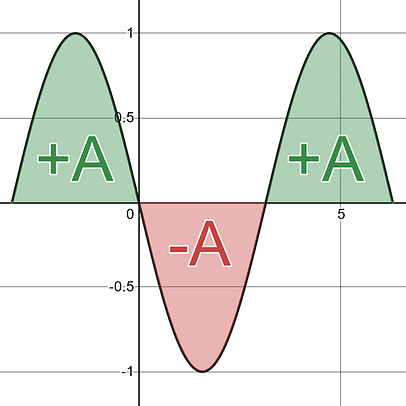
With net accumulation you treat area above the x-axis as positive amounts and area below the x-axis as negative amounts. You then add all those areas together to get your Net Accumulation. |
With total area you treat ALL area as positive area. You do not care about above or below the x-axis . You want to know the full value of ALL the area between the curve and the x-axis , the Total Area. This value will always be positive or zero. |
|
|
|
|
Net Area = A– A+ A = +1A |
Total Area = A + A + A = +3A |
|
Real World : You would refer to this as your Net displacement . You took one meter forward, then one meter back, and then one meter forward. Therefore, your Netdisplacement is that you have moved forward 1 meter from your starting location. |
Real World : You would refer to this as your Total distance traveled . . You took one meter forward, then one meter back, and then one meter forward. Therefore, you traveled a Total of 3 meters since you left your starting location. |