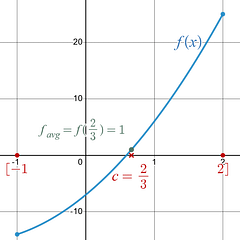
Example 1: Mean Value Theorem for Definite Integrals

Determine x-value of $f\left(x\right)={3x}^2+10x–7$ on the interval $\left[–1,2\right]$ that fulfills the Mean Value Theorem for Definite Integrals.

Step 1: Determine the Average Value, $f_{\mathit{avg}}$, of your given equation, $f\left(x\right)$, over the given the x-interval , [ a , b ] using the Average Value formula.

[ a , b ] = [ -1 , 2 ]

$f\left(x\right)={3x}^2+10x–7$

Solve the Definite Integral using the power rule.

$\underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}\mathit{=}\mathit{3}$

Simplify the fraction in the front.

$\frac{1}{2–(–1)}=\frac{1}{3}$

$f_{\mathit{avg}}=\frac{1}{b–a}\bullet \underset{a}{\overset{b}{\int }}f\left(x\right) \mathit{dx}$

$f_{\mathit{avg}}=\frac{1}{2–(–1)}\bullet \underset{–1}{\overset{2}{\int }}{3x}^2+10x–7 \mathit{dx}$

$f_{\mathit{avg}}=\frac{1}{3}\bullet \mathit{3}$

$f_{\mathit{avg}}=1$

Step 2: Set your given equation, $f\left(x\right)$, equal to the average value you found in Step 1 , $f_{\mathit{avg}}$, and solve for x (i.e., get x alone on side of the equals).

When solving a quadratic or higher power equation, the method is generally the same.

1)      Get the equation set equal to zero.

2)      Factor the equation.

3)      Set the factors equal to zero and solve those smaller math problems to find your possible solutions.

After you find your possible solutions remember that you will need to check that they are inside your given interval, [ a , b ] = [ -1 , 2 ]. If they are in your interval keep them. If they are not in your interval get rid of them.

$f\left(x\right)={3x}^2+10x–7$

$f_{\mathit{avg}}=1$

${3x}^2+10x–7=1$

${3x}^2+10x\begin{array}{c}–7\\ –1\end{array}=\begin{array}{c}1\\ –1\end{array}$

${3x}^2+10x–8=0$

$\left(3x–2\right)\left(x+4\right)=0$

$\left(3x–2\right)=0$          $\left(x+4\right)=0$

$3x\begin{array}{c}–2\\ +2\end{array}=\begin{array}{c}0\\ +2\end{array}$             $x+\begin{array}{c}+4\\ –4\end{array}=\begin{array}{c}0\\ –4\end{array}$

$3x=2$             $x=–4$

$3x=2$             $x=–4$

$\frac{3}{3}x=\frac{2}{3}$             $x=–4$

$x=\frac{2}{3}$             $x=–4$

$x=\frac{2}{3}$             $x=–4$

Good: $\overline{)x=\frac{2}{3}}$            Bad: $\overline{)x=–4}$

Meaning of the Final Result:

The c-value guaranteed by the Mean Value Theorem for Definite Integrals in the given x-interval , [ -1 , 2 ], is $x=\frac{2}{3}$.

This tells you that if you plug $x=\frac{2}{3}$into the given equation $f\left(x\right)={3x}^2+10x–7$, then the y-value that you get out will be equal to the average y-value of $f\left(x\right)$ over the interval [ -1 , 2 ].

$f_{\mathit{avg}}=1$

$f\left(\frac{2}{3}\right)=1$

$f_{\mathit{avg}}=f\left(\frac{2}{3}\right)=1$