Using Cross Sectional Areas

Unit 8: Applications of Antiderivatives Using Cross Sectional Areas

There are 3 integration methods for finding the volume of a solid, a shape; Cross Sectional Areas, Disk Method, and Washer Method. Each of the 3 integration methods are really just 3 different integration formulas that you have to know. Once you know the integration formulas , you plug in your specific problem’s information, and complete the process by calculating a Definite Integral.

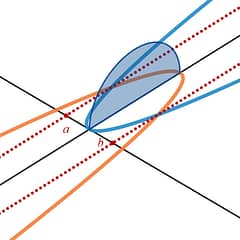
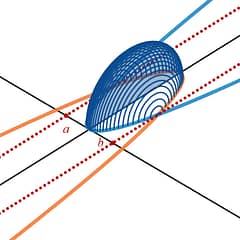
The first integration formula you learn about is called Cross Sectional Areas. The name of this method is a bit confusing since it says area , but we are using it to find volumes . The best way to think of this method is think of it as a loaf of bread. You will find the area of the slices of bread, and then add up all the slices to find the volume of the loaf.

Definition: Volumes using Cross Sectional Areas

The integration formula for finding the volume of a solid using Cross Sectional Areas is

$Volume = \int_{a}^{b} A (x) dx$

What it means:

Again, try to think about this method in terms of a loaf of bread. The slices of bread are the area formula , A(x) , and the volume of the loaf of bread comes from adding up all the slices. You add up all the slices using your antiderivative, which is an accumulation tool, and the bounds of that antiderivative, [ a , b ], are the length of your x-interval , or the length of your loaf of bread, $\int_{a}^{b}$ .

$Loaf = \int_{a}^{b} Slices dx$

Single Slice of Bread = A(x)

More Slices of Bread = A(x)

Loaf of Bread = $\int_{a}^{b} A (x) dx = Volume$

Add up all the slices and you obtain the volume.

The area formula, A(x) , is really the key to the setup here. These area formulas will usually be one of your standard geometric shapes (i.e., circles, squares, triangles).

EX:
$A (x) = Standard Geometric Area Formula$

$A (x) = Area of Circle = π r^{2}$