Example 1: About the x-axis

Find the volume of the solid generated by revolving the region bounded by the curves $y=x^2+2,\mathit{ x}=–2,\mathit{ x}=2$ about the x-axis .

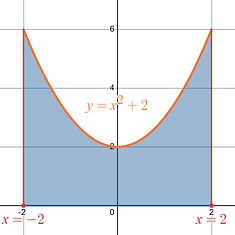
Step 1: Draw out the region that you are being asked to rotate.

In this example you have the curve, $y=x^2+2$, which is a parabola shifted up two units, and you close off the region on the lefthand and righthand sides using the curves, $x=–2, x=2$.

The region that you are being asked to rotate is the shaded region.

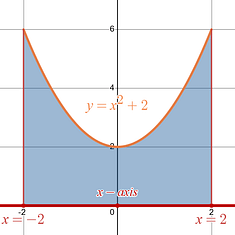
Step 2: Determine the axis you are begin asked to revolve or rotate your region around.

In this problem the language says, “about the x-axis ”. You are revolving around the x-axis .

Step 3: Determine whether your equation is in terms of x (standard: $y=x^2+3x+\sqrt{x}$) or in terms of y (non-standard: $x=y^2+3y+\sqrt{y}$).

Since you are asked to revolve around the x-axis you know that this is a horizontal axis , and you want to setup your Disk Methodintegral in terms of x .

The given equation , $y=x^2+2$, is ready to use because it is already in terms of x .

Step 4: Determine the bounds of the integral, $\underset{a}{\overset{b}{\int }}$, for each of your enclosed regions.

This problem gives your bounds in the form of the two additional equations, $x=–2,\mathit{ x}=2$, that close the region on the lefthand and righthand sides.

The lower bound will be a = -2 , and the upper bound of your integral will be b = 2 .

$\underset{a}{\overset{b}{\int }}=\underset{–2}{\overset{2}{\int }}$

Step 5: Determine your radius equation, $R\left(x\right)$.

If you are rotating strictly around the standard x-axis or the y-axis , then the given equation you are asked to rotate is your R(x) equation.

Since you are being asked to rotate about the x-axis in this problem, the given equation, $y=x^2+2$, is your R(x) equation.

$R\left(x\right)=x^2+2$

Step 6: Setup up and evaluate your Disk Methodintegral.

Use the results of Step 4 (your bounds ) and Step 5 (your R(x) equation) together using the Disk Methodintegral setup.

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}\pi {\left[R\left(x\right)\right]}^2\mathit{dx}$

The first step in evaluating these Disk Methodintegral will usually be to expand the squared term.

Once you have expanded the squared term, you can factor out (pull to the front) the $\pi$, and then multiply it by the final result of the definite integral at the end of the process.

You will generally be able to handle the definite integral using only the Power Rule.

– Bounds from Step 4 : $\underset{–2}{\overset{2}{\int }}$

– R(x) equation from Step 5 : $R\left(x\right)=x^2+2$

$\mathit{Volume}=\underset{–2}{\overset{2}{\int }}\pi {\left[x^2+2 \right]}^2\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^2+2\right)\left(x^2+2\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4+2x^2+2x^2+4\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4+4x^2+4\right)\mathit{dx}$

$=\pi \bullet \underset{–2}{\overset{2}{\int }}\left(x^4+4x^2+4\right)\mathit{dx}$

$\mathit{=}\pi \bullet \left({\frac{x^5}{5}+\frac{4x^3}{3}+4x|}_{–2}^2\right)$

$\mathit{=}\pi \bullet \left(\left[\frac{{\left(2\right)}^5}{5}+\frac{4{\left(2\right)}^3}{3}+4\left(2\right)\right]–\left[\frac{{\left(–2\right)}^5}{5}+\frac{4{\left(–2\right)}^3}{3}+4\left(–2\right)\right]\right)$

$\mathit{=}\pi \bullet \left(\frac{752}{15}\right)$

$\mathit{=}\frac{752}{15}\pi =\mathit{Volume\; of\; Solid}$

Final Result:

The volume of the solid obtained by rotating the region bounded by the curves $y=x^2+2, x=–2,x=2$ about the x-axis is $\frac{752}{15}\pi$.