Washer Method

Definition: Volumes of Solids (Rotation): Washer Method

The Washer Method is really just a combination of the Disk Method and Area Between Two Curves Method. You are taking the Area Between Two Curves and rotating that shape 360 ^◦ around an axis, just like you did with Disk Method.

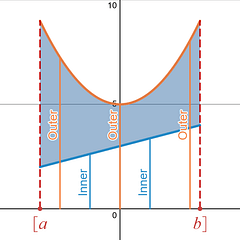
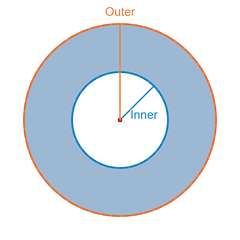
Similar to the Area Between Two Curves Method (Top minus Bottom)with the Washer Method you have an Outer Disk (Top Curve) and you are subtracting from that the Inner Disk (Bottom Curve). In the end you are left with a Washer (i.e., a Disk with a hole subtracted out of the middle).

The Washer Method integration formula for finding the volume of a solid rotated around an axis is

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}\pi \left({\left[R\left(x\right)\right]}^2–{\left[r\left(x\right)\right]}^2\right)\mathit{dx}=\underset{a}{\overset{b}{\int }}\pi \left({\left[\mathit{Outter}\right]}^2–{\left[\mathit{Inner}\right]}^2\right)\mathit{dx}$

What it means:

When you look at this formula what it should look like is two area of a circle equations, $A=\pi r^2$, being subtracted, because that is exactly what is happening. They just factor the $\pi$ out of the two equations.

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}{\pi \left[R\left(x\right)\right]}^2–\pi {\left[r\left(x\right)\right]}^2\mathit{dx}=\underset{a}{\overset{b}{\int }}\pi \left({\left[R\left(x\right)\right]}^2–{\left[r\left(x\right)\right]}^2\right)\mathit{dx}$

The equations you are given to rotate around an axis will be what creates the radius of your disks or circles , the Outer radius , R(x) , and the Inner radius , r(x) . Again, the more you can think about these two equations in the same way you did with the Area Between Two Curves Method, Top = Outer and Bottom = Inner , the happier you will be.

The slices of bread are those washers ( disks with a hole ), and the volume of the loaf of bread comes from adding up all the slices, all your washers .

You add up all the disks using your antiderivative, which is an accumulation tool, and the bounds of that antiderivative, [ a , b ], are the length of your x-interval , or the length of your loaf of bread, $\underset{a}{\overset{b}{\int }}$.

$\mathit{Loaf}=\underset{a}{\overset{b}{\int }}\mathit{Slices}\mathit{dx}$