Example 1: Washer Method About the x-axis

Find the volume of the solid generated by revolving the region bounded by the curves $y=x^2+5,\mathit{ y}=\frac{1}{2}x+3,\mathit{ x}=–2,\mathit{ x}=2$ about the x-axis.

Step 1: Draw out the region that you are being asked to rotate .

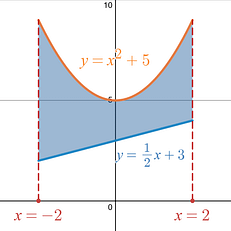
In this example you have the curve $y=x^2+5$, which is a parabola shifted up two units, the curve $y=\frac{1}{2}x+3$, which is a linear equation with a y-intercept of 3 and a slope of 3. You close off the region on the lefthand and righthand sides using the curves, $x=–2, x=2$.

The region that you are being asked to rotate is the shaded region.

Step 2: Determine the axis you are begin asked to revolve or rotate your region around.

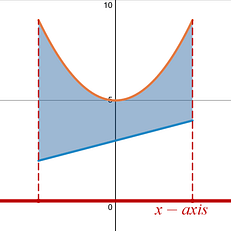
In this problem the language says, “about the x-axis ”. You are revolving around the x-axis .

Step 3: Determine whether your equation is in terms of x (standard: $y=x^2+3x+\sqrt{x}$) or in terms of y (non-standard: $x=y^2+3y+\sqrt{y}$).

Since you are asked to revolve around the x-axis you know that this is a horizontal axis , and you want to setup your Disk Methodintegral in terms of x .

The given equations , $y=x^2+5$ and are $y=\frac{1}{2}x+3$ready to use because it is already in terms of x .

Step 4: Determine the bounds of the integral, $\underset{a}{\overset{b}{\int }}$, for each of your enclosed regions.

This problem gives your bounds in the form of the two additional equations, $x=–2,\mathit{ x}=2$, that close the region on the lefthand and righthand sides.

The lower bound will be a = -2 , and the upper bound of your integral will be b = 2 .

$\underset{a}{\overset{b}{\int }}=\underset{–2}{\overset{2}{\int }}$

Step 5: Determine your radius equations, the Outer radius , R(x) , and the Inner radius , r(x) .

I find it helpful to draw the two radiuses. Start on the axis of rotation you are provided, and draw a line towards the region that you drew in Step 1 .

Since you are rotating around the standard x-axis , start on the x-axis , and draw up. The graph that you run into first is your Inner radius , r(x) , and the graph that you run into second is your Outer radius , R(x) .

Here the first curve you run into is $y=\frac{1}{2}x+3$, and the second curve you would run into would be $y=x^2+5$.

$\mathit{Inner}=r\left(x\right)=\frac{1}{2}x+3$

$\mathit{Outter}=R\left(x\right)=x^2+5$

Step 6: Setup and evaluate your Washer Methodintegral.

– Bounds from Step 4 : $\underset{–2}{\overset{2}{\int }}$

– Equations from Step 5 : $\mathit{Inner}=r\left(x\right)=\frac{1}{2}x+3$

$\mathit{Outter}=R\left(x\right)=x^2+5$

$\mathit{Volume}=\underset{a}{\overset{b}{\int }}\pi \left({\left[R\left(x\right)\right]}^2–{\left[r\left(x\right)\right]}^2\right)\mathit{dx}=\underset{a}{\overset{b}{\int }}\pi \left({\left[\mathit{Outter}\right]}^2–{\left[\mathit{Inner}\right]}^2\right)\mathit{dx}$

$\mathit{Volume}=\underset{–2}{\overset{2}{\int }}\pi \left({\left[x^2+5\right]}^2–{\left[\frac{1}{2}x+3\right]}^2\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(\left(x^2+5\right)\left(x^2+5\right)–\left(\frac{1}{2}x+3\right)\left(\frac{1}{2}x+3\right)\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(\left(x^4+5x^2+5x^2+25\right)–\left(\frac{1}{4}{x}^2+\frac{3}{2}x+\frac{3}{2}x+9\right)\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(\left(x^4+10x^2+25\right)–\left(\frac{1}{4}{x}^2+3x+9\right)\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(\left(x^4+10x^2+25\right)–\left(\frac{1}{4}{x}^2+3x+9\right)\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(\left(x^4+10x^2+25\right)\mathit{–}\frac{1}{4}{x}^2\mathit{–}3x\mathit{–}9\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4+10x^2+25\mathit{–}\frac{1}{4}{x}^2\mathit{–}3x\mathit{–}9\right)\mathit{dx}$

$=\underset{–2}{\overset{2}{\int }}\pi \left(x^4+\frac{39}{4}{x}^2\mathit{–}3x\mathit{+}\mathit{16}\right)\mathit{dx}$

$=\pi \bullet \underset{–2}{\overset{2}{\int }}\left(x^4+\frac{39}{4}{x}^2\mathit{–}3x\mathit{+}\mathit{16}\right)\mathit{dx}$

$=\pi \bullet \left({\frac{x^5}{5}+\frac{39}{4}\bullet \frac{x^3}{3}–\frac{3x^2}{2}+16x|}_{–2}^2\right)\mathit{=}$

$\pi \bullet \left(\left[\frac{{\left(2\right)}^5}{5}+\frac{39}{4}\bullet \frac{{\left(2\right)}^3}{3}–\frac{3{\left(2\right)}^2}{2}+16\left(2\right)\right]–\left[\frac{{\left(–2\right)}^5}{5}+\frac{39}{4}\bullet \frac{{\left(–2\right)}^3}{3}–\frac{3{\left(–2\right)}^2}{2}+16\left(–2\right)\right]\right)=$

$\pi \bullet \left(\frac{644}{5}\right)=$

$\frac{644}{5}\pi =\mathit{Volume\; of\; Solid}$

The volume of the solid obtained by rotating the region bounded by the curves $y=x^2+2,\mathit{ }y=\frac{1}{2}x+3,\mathit{ }x=–2,\mathit{ }x=2$ about the x-axis is $\frac{644}{5}\pi$.