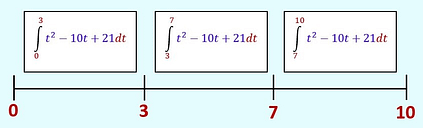Example 1: Distance vs. Displacement

You are walking along a straight path, and your velocity, in meters per minute, can be modeled by $v\left(t\right)=t^2–10t+21$ for $0\le t\le 10$ minutes.

a)       What is your displacement over the interval $0\le t\le 10$ minutes?

b)      How far did you walk in total over the interval $0\le t\le 10$ minutes?

Step 1: Identify whether you are being asked to find the Displacement or the Distance Traveled.

Here you are being asked to find both the Displacement and the Distance Traveled.

a)       Uses the exact word displacement , which tells you that you need to find your displacement over the given interval.

b)      Uses the word total , and is talking about how much you walked overall . This would be the Distance Traveled.

a)       What is your displacement over the interval $0\le t\le 10$ minutes?

b)      How far did you walk in total over the interval $0\le t\le 10$ minutes?

Step 2 ( Displacement ): Setup and evaluate a Definite Integral problem using the given velocity equation, v(t) , and the given time interval, [ a , b ].

[ a , b ] = [ 0 , 10 ]

$v\left(t\right)=t^2–10t+21$

After setting up the Definite Integral you would apply the Power Rule, and then use your Top–Bottom process to find your final result.

$\underset{0}{\overset{10}{\int }}{t}^2–10t+21 \mathit{dt}=\mathit{Displacement}$

${\frac{t^3}{3}–\frac{{10t}^2}{2}+21t|}_0^{10}\mathit{=}$

$\left[\frac{{\left(10\right)}^3}{3}–\frac{{10\left(10\right)}^2}{2}+21\left(10\right)\right]–\left[\frac{{\left(0\right)}^3}{3}–\frac{{10\left(0\right)}^2}{2}+21\left(0\right)\right]=\frac{130}{3}\mathit{meters}$

$\mathit{Displacement}=\frac{130}{3}\mathit{meters}$

Step 2 ( Total Distance ): Set your velocity equation equal to zero, v(t) = 0 ,and solve for the times ( x-values ) that your equation could changes signs (+/–).

This tells you that you would break your x-values [ 0 , 10 ], and into smaller subintervals at the x-values you just found.

$v\left(t\right)=t^2–10t+21$

$0=t^2–10t+21$

$0=\left(t–3\right)\left(t–7\right)$

$0=\left(t–3\right)$ and $0=\left(t–7\right)$

$t=3$ and $t=7$

Step 3 ( Total Distance ): Setup and evaluate the Definite Integrals based upon the smaller x-intervals you found in Step 2 (Total Distance).

$\underset{0}{\overset{3}{\int }}{t}^2–10t+21 \mathit{dt}$

${\frac{t^3}{3}–\frac{{10t}^2}{2}+21t|}_0^3\mathit{=}$

$\left[\frac{{\left(3\right)}^3}{3}–\frac{{10\left(3\right)}^2}{2}+21\left(3\right)\right]–\left[\frac{{\left(0\right)}^3}{3}–\frac{{10\left(0\right)}^2}{2}+21\left(0\right)\right]$

$=27\mathit{meters}$

$\underset{3}{\overset{7}{\int }}{t}^2–10t+21 \mathit{dt}$

${\frac{t^3}{3}–\frac{{10t}^2}{2}+21t|}_3^7\mathit{=}$

$\left[\frac{{\left(7\right)}^3}{3}–\frac{{10\left(7\right)}^2}{2}+21\left(7\right)\right]–\left[\frac{{\left(3\right)}^3}{3}–\frac{{10\left(3\right)}^2}{2}+21\left(3\right)\right]$

$=–\frac{32}{3}\mathit{meters}$

$\underset{7}{\overset{10}{\int }}{t}^2–10t+21 \mathit{dt}$

${\frac{t^3}{3}–\frac{{10t}^2}{2}+21t|}_7^{10}\mathit{=}$

$\left[\frac{{\left(10\right)}^3}{3}–\frac{{10\left(10\right)}^2}{2}+21\left(10\right)\right]–\left[\frac{{\left(7\right)}^3}{3}–\frac{{10\left(7\right)}^2}{2}+21\left(7\right)\right]$

$=27\mathit{meters}$

Step 4 ( Total Distance ): Treat all results from Step 3 (Total Distance) as positive values, and then add those results together to get your final result for Total Distance.

$\mathit{Total\; Distance\; Traveled}=27\mathit{meters}+\left|–\frac{32}{3}\mathit{meters}\right|+27\mathit{meters}$

$\mathit{Total\; Distance\; Traveled}=27\mathit{meters}+\frac{32}{3}\mathit{meters}+27\mathit{meters}$

$\mathit{Total\; Distance\; Traveled}=\frac{194}{3}\mathit{meters}$

Final Results:

After traveling in a straight line for 10 minutes at a velocity of $v\left(t\right)=t^2–10t+21$, you are $\frac{130}{3}\mathit{meters}$ from your starting position, and you traveled a total distance of $\frac{194}{3}\mathit{meters}$.