Riemann Sums Become Definite Integrals

Riemann Sum vs. Integral

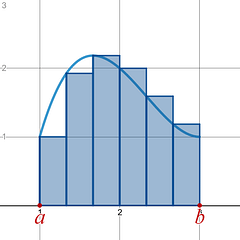
Riemann Sum

Uses shapes (usually rectangles, but could be any shape) to estimate the net area between a curve and the x-axis on a given x-interval [ a , b ].

In the example below the interval [1,3] was broken up into 6 subintervals,$\mathit{n}\mathit{=}\mathit{6}$. As you can see there are always going to be some over and under estimates when using geometric shapes. What you inevitably get out is an estimate of the net area between a curve and the x-axis .

Extension

As you increase the number, n ,of subintervals over the same x-interval [ a , b ], you will see that your over and under estimates of the area between a curve and the x-axis become smaller, and the Riemann Sum continues to get more accurate.

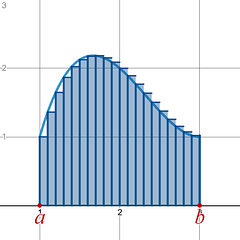
Definite Integral

Uses integration rules to find the exact net area between a curve and the x-axis on a given x-interval [ a , b ].

The Definite Integral, exact net area between a curve and the x-axis , applies a Limit to break up the x-interval [ a , b ] into an infinite number of subintervals, $\mathit{n}\mathit{=}\mathit{\infty }$.

Since each subinterval is as close to the next subintervals as it can possibly be, the $∆x\to 0$, and you no longer have any over or under estimates , and get out an exact net area between a curve and the x-axis on a given x-interval [ a , b ].

$\mathit{n}\mathit{=}\mathit{6}$

$\mathit{n}\mathit{=}\mathit{20}$

$\mathit{n}\mathit{=}\mathit{\infty }$