Net Area vs Total Area
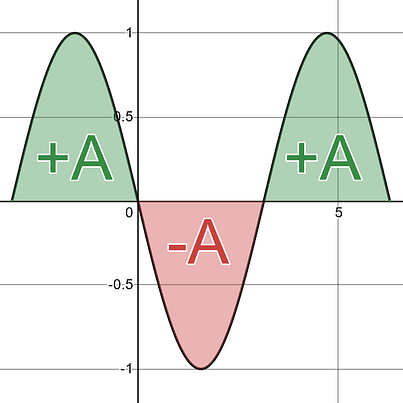
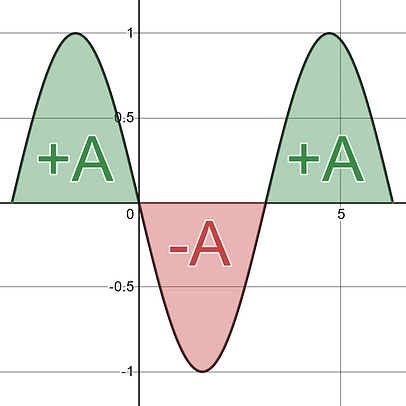
One major distinction you will need to pay close attention to on any Definite Integral problem is whether the problem is asking you to find the Net Area or the Total Area between the curve and the x-axis . Remember that area above the x-axis is considered positive area, and area below the x-axis is considered negative area. It is how the negative area is handled that is the distinction between the two terms.
|
Total Area = Total Distance Traveled |
|
|
With net area you treat area above the x-axis as positive area and area below the x-axis as negative area. You then add all those areas together to get your Net Area. |
With total area you treat ALL area as positive area. You do not care about above or below the x-axis . You want to know the full value of ALL the area between the curve and the x-axis , the Total Area. This value will always be positive or zero. |
|
|
|
|
Net Area = A– A+ A = +1A |
Total Area = A + A + A = +3A |
|
Real World : You would refer to this as your Net displacement . You took one step forward, then one step back, and then one step forward. Therefore, your Netdisplacement is that you have moved forward 1 step from your starting location. |
Real World : You would refer to this as your Total distance traveled . You took two steps forward and one step back, and therefore you traveled a Total of 3 steps since you left your starting location. |