Example 1: Indefinite Integral Power Rule
|
|
|||||
|
Step 1: Simplify and look for algebraic rewrites.
When looking at the first chunk Remind yourself that there is really an unwritten 1 for the power. That is what allows us to apply the power rule . |
|
||||
|
Step 2: Identify any term(s) that include variables raised to a power. Break the problem down into bitesize chunks based upon the + and – , and identify the antiderivative rule for each chunk (term).
Here you have 2 chunks. The first chunk, 6x , will be a power rule , and the second chunk, 9, is a constant. |
|
||||
|
Step 3: Take the antiderivativeof the variables raised to a power using the Recipe:Add 1 to the power; Divide by the new power.
Chunk 1: Power Rule Chunk 2: Constant Rule |
DO NOT FORGET THE +C |
||||
|
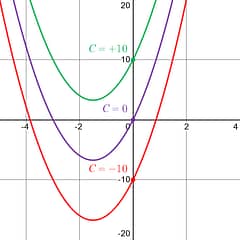
Final Result Meaning: Remember the Definite Integral will always provide you a definite value , and the Indefinite Integral provides you a family of solutions . |
The antiderivative of the equation is the family of graphs .
All graphs of the form have the same derivative (instantaneous rate of change), , at any x-value . The only difference between any of original graphs, , is just a vertical shift of +C . In the graph above are examples of 3-different C-values. You can see the instantaneous rate of change ( slope ) is the same at every x-value between all the different examples, no matter the +C . |
||||