Example 1: Indefinite Integral U-Substitution

Actual Work

Side Work

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

Step 1: Simplify and look for algebraic rewrites.

None in this example.

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

Step 2 (Beginning of the side work) : Choose your u .

Going through The U Priority List to help decide on your u .

Priority 1: $\mathit{ln}\left(x\right)$

You don’t have $\mathit{ln}\left(x\right)$.

Priority 2: The Inside piece.

You do have an inside piece here. The $x^3+{5x}^2$ term is inside the 3 ^rd power, ${\left(\right)}^3$.

It also fits the General Priority: The piece with the highest power of x .

$x^3$ is the highest power of x in the main integral.

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

$u\mathit{=}{x}^3+{5x}^2$

Step 3 (Side work) : Take the derivative of your u , and always use differential notation to represent the derivative (i.e., $\frac{\mathit{dy}}{\mathit{dx}}$, not $f\prime \left(x\right)$).

$\frac{\mathit{du}}{\mathit{dx}}={3x}^2+10x$

Step 4 (Side work) : Solve the derivative you just created for $\mathit{dx}$.

1)      Multiply both sides by $\mathit{dx}$ to get the $\mathit{dx}$ out of the bottom of the fraction.

2)      Divide both sides by ${3x}^2+10x$ to get $\mathit{dx}$ by itself.

$\mathit{dx}\bullet \left(\frac{\mathit{du}}{\mathit{dx}}\right)=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\mathit{dx}\bullet \left(\frac{\mathit{du}}{\mathit{dx}}\right)=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\mathit{du}=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\frac{\left({3x}^2+10x\right)\bullet \mathit{dx}}{\left({3x}^2+10x\right)}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\frac{\left({3x}^2+10x\right)\bullet \mathit{dx}}{\left({3x}^2+10x\right)}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\mathit{dx}$

Step 5 (Side work for Definite Integrals only ): Adjust the original bounds, $\underset{a}{\overset{b}{\int }}$ of your main integral.

SKIP: Indefinite Integral no bounds

Step 6: Substitute back into your main integral.

You work your way through your main integral left to right, and each piece in the main integral is either one of the pieces you are substituting from your side work or it stays.

–           Substitute in u for the piece that you chose as your u in Step 1 .

–           Substitute in for the $\mathit{dx}$what you found in Step 4 .

Working through the main integral left to right, nothing happens to the $\left({3x}^2+10x\right)$ piece, you substitute in u for the $x^3+{5x}^2$ piece, and you substitute $\frac{\mathit{du}}{\left({3x}^2+10x\right)}$ for $\mathit{dx}$.

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3\mathit{ dx}$

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

$\int \left({3x}^2+10x\right){\left(u\right)}^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$u\mathit{=}{x}^3+{5x}^2$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\mathit{dx}$

Step 7: Simplify the updated main integral you just substituted into.

As you would hope, the ${3x}^2+10x$ that was left in the main integral will cancel out with the ${3x}^2+10x$that was a part of the u that got substituted into the main integral.

How convenient.

$\int \left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\int \left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\int \left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\int u^3\mathit{ du}$

Step 8: Treat the simplified main integral from Step 7 like a brand-new math problem , and begin your standard antiderivative methods.

Here you are now looking at a straightforward Power Rule :

Step 1: Add 1 to the power.

Step 2: Divide by the new power.

$\int u^3\mathit{ du}$

$\int u^3\mathit{ du}=\frac{u^{3+1}}{4}\mathbf{+}\mathbf{C}\mathbf{=}\frac{u^4}{4}\mathbf{+}\mathbf{C}$

$\int u^3\mathit{ du}=\frac{u^4}{4}\mathbf{+}\mathbf{C}$

Step 9 (Indefinite Integrals only ) : Substitute back in for the u ’s in the antiderivative result.

$\int u^3\mathit{ du}=\frac{u^4}{4}\mathbf{+}\mathbf{C}\mathbf{=}\frac{{\left(x^3+{5x}^2\right)}^4}{4}\mathbf{+}\mathbf{C}$

$u\mathit{=}{x}^3+{5x}^2$

Final Result:

$\int \left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

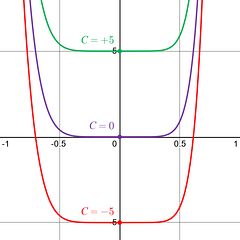
The antiderivative of the equation $f\prime \left(x\right)=\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3$is the family of graphs $f\left(x\right)=\frac{{\left(x^3+{5x}^2\right)}^4}{4}\mathbf{+}\mathbf{C}$.

All graphs of the form $f\left(x\right)=\frac{{\left(x^3+{5x}^2\right)}^4}{4}\mathbf{+}\mathbf{C}$ have the same derivative (instantaneous rate of change), $f\prime \left(x\right)=\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3$, at any x-value .

The only difference between any of original graphs, $f\left(x\right)=\frac{{\left(x^3+{5x}^2\right)}^4}{4}\mathbf{+}\mathbf{C}$, is just a vertical shift of +C .

In the graph above are examples of 3-different C-values. You can see the instantaneous rate of change ( slope ) is the same at every x-value between all the different examples, no matter the +C .