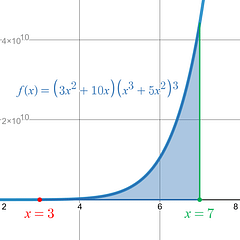
Example 2: Definite Integral U-Substitution

Actual Work

Side Work

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3\mathit{ dx}$

Step 1: Simplify and look for algebraic rewrites.

None in this example.

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3\mathit{ dx}$

Step 2 (Beginning of the side work) : Choose your u .

Going through The U Priority List to help decide on your u .

Priority 1: $\mathit{ln}\left(x\right)$

You don’t have $\mathit{ln}\left(x\right)$.

Priority 2: The Inside piece.

You do have an inside piece here. The $x^3+{5x}^2$ term is inside the 3 ^rd power, ${\left(\right)}^3$.

It also fits the General Priority: The piece with the highest power of x .

$x^3$ is the highest power of x in the main integral.

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3\mathit{ dx}$

$u\mathit{=}{x}^3+{5x}^2$

Step 3 (Side work) : Take the derivative of your u , and always use differential notation to represent the derivative (i.e. $\frac{\mathit{dy}}{\mathit{dx}}$, not $f\prime \left(x\right)$).

$\frac{\mathit{du}}{\mathit{dx}}={3x}^2+10x$

Step 4 (Side work) : Solve the derivative you just created for $\mathit{dx}$.

1)      Multiply both sides by $\mathit{dx}$ to get the $\mathit{dx}$ out of the bottom of the fraction.

2)      Divide both sides by ${3x}^2+10x$ to get $\mathit{dx}$ by itself.

$\mathit{dx}\bullet \left(\frac{\mathit{du}}{\mathit{dx}}\right)=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\mathit{dx}\bullet \left(\frac{\mathit{du}}{\mathit{dx}}\right)=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\mathit{du}=\left({3x}^2+10x\right)\bullet \mathit{dx}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\frac{\left({3x}^2+10x\right)\bullet \mathit{dx}}{\left({3x}^2+10x\right)}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\frac{\left({3x}^2+10x\right)\bullet \mathit{dx}}{\left({3x}^2+10x\right)}$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\mathit{dx}$

Step 5 (Side work for Definite Integrals only ): Adjust the original bounds, $\underset{3}{\overset{7}{\int }}$ of your main integral.

Adjusting the upper bound, x = 7 .

$u\mathit{=}{x}^3+{5x}^2$

$u\mathit{=}{\left(7\right)}^3+{5\left(7\right)}^2=588$

New upper bound, u = 588 .

Adjusting lower bound, x = 3 .

$u\mathit{=}{x}^3+{5x}^2$

$\mathit{u}\mathit{=}{\left(3\right)}^3+{5\left(3\right)}^2=72$

New lower bound, u = 72 .

Step 6: Substitute back into your main integral.

You work your way through your main integral left to right, and each piece in the main integral is either one of the pieces you are substituting from your side work or it stays.

–           Substitute in u for the piece that you chose as your u in Step 1 .

–           Substitute in for the $\mathit{dx}$what you found in Step 4 .

–           Substitute in your new upper and lower bounds that you found in Step 5 .

Working through the main integral left to right, nothing happens to the $\left({3x}^2+10x\right)$ piece, you substitute in u for the $x^3+{5x}^2$ piece, and you substitute $\frac{\mathit{du}}{\left({3x}^2+10x\right)}$ for $\mathit{dx}$.

Since you have a definite integral, you will also substitute in your new upper bound, u = 588 , and new lower bound, u = 72 .

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3 \mathit{dx}$

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(u\right)}^3 \mathit{dx}$

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(u\right)}^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\underset{72}{\overset{588}{\int }}\left({3x}^2+10x\right){\left(u\right)}^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$u\mathit{=}{x}^3+{5x}^2$

$\frac{\mathit{du}}{\left({3x}^2+10x\right)}=\mathit{dx}$

New upper bound, u = 588 .

New lower bound, u = 72 .

Step 7: Simplify the updated main integral you just substituted into.

As you would hope, the ${3x}^2+10x$ that was left in the main integral will cancel out with the ${3x}^2+10x$that was a part of the u that got substituted into the main integral.

How convenient.

$\underset{72}{\overset{588}{\int }}\left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\underset{72}{\overset{588}{\int }}\left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\underset{72}{\overset{588}{\int }}\left({3x}^2+10x\right)\bullet u^3 \frac{\mathit{du}}{\left({3x}^2+10x\right)}$

$\underset{72}{\overset{588}{\int }}{u}^3\mathit{ du}$

Step 8: Treat the simplified main integral from Step 7 like a brand-new math problem , and begin your standard antiderivative methods.

Here you are now looking at a straightforward Power Rule :

Step 1: Add 1 to the power.

Step 2: Divide by the new power.

$\underset{72}{\overset{588}{\int }}{u}^3\mathit{ du}$

$\underset{72}{\overset{588}{\int }}{u}^3\mathit{ du}={\frac{u^{3+1}}{4}|}_{u=72}^{u=588}\mathbf{=}{\frac{u^4}{4}|}_{u=72}^{u=588}$

$\underset{72}{\overset{588}{\int }}{u}^3\mathit{ du}\mathbf{=}{\frac{u^4}{4}|}_{u=72}^{u=588}$

Step 9 (Definite Integrals only ) : Evaluate the antiderivative at the bounds of your integral.

You need to finish evaluating like you would on any Definite Integral problem using the Top – Bottom method. Plug the upper bound into your antiderivative and subtract off the lower bound plugged into your antiderivative.

$\underset{72}{\overset{588}{\int }}{u}^3\mathit{ du}\mathbf{=}{\frac{u^4}{4}|}_{u=72}^{u=588}\mathit{=}\frac{{\left(588\right)}^4}{4}–\frac{{\left(72\right)}^4}{4}=29,878,009,920$

Final Result:

$\underset{3}{\overset{7}{\int }}\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3\mathit{ dx}$

The Net Area between the curve $f\left(x\right)=\left({3x}^2+10x\right){\left(x^3+{5x}^2\right)}^3$ and the x-axis on the x-interval [ 3 , 7 ] is 29,878,009,920 .

Since the final result is positive, you know without even seeing the graph that there is more area above the x-axis than below it.