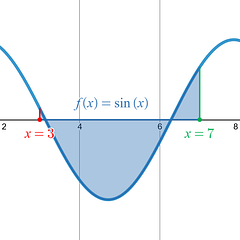
Example 1: Definite Integral Trig Function

$\underset{3}{\overset{7}{\int }}\mathit{sin}\left(x\right)\mathit{ dx}$

Step 1: Simplify and look for algebraic rewrites.

None in this example.

$\underset{3}{\overset{7}{\int }}\mathit{sin}\left(x\right)\mathit{ dx}$

Step 2: Identify any term(s) that include one of the six trig function special cases.

Here you have 1 chunk, and it is one of the trig function special cases.

$\underset{3}{\overset{7}{\int }}\mathit{sin}\left(x\right)\mathit{ dx}$

Step 3: Take the antiderivativeof the trig function special cases using their specific Recipe.

Chunk 1: sin(x)

$\underset{3}{\overset{7}{\int }}\mathit{sin}\left(x\right)\mathit{ dx}\mathit{=}{–\mathit{cos}\left(x\right)|}_{x=3}^{x=7}$

Step 4 ( Definite Integral ONLY ): Evaluate the antiderivative result using the Top – Bottom method.

$\underset{3}{\overset{7}{\int }}\sin \left(x\right)\mathit{dx}={–\cos \left(x\right)|}_{x=3}^{x=7}$

$=\left(–\mathit{cos}\left(7\right)\right)–\left(–\mathit{cos}\left(3\right)\right)\approx –1.743$

Final Result Meaning: Remember the Definite Integral will always provide you a definite value , and the Indefinite Integral provides you a family of solutions .

The Net Area between the curve $f\left(x\right)=\mathit{sin}\left(x\right)$ and the x-axis on the x-interval [ 3 , 7 ] is -1.743 .

Since the final result is negative, you know without even seeing the graph that there is more area below the x-axis than above it.