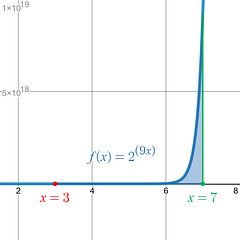
Example 1: Definite Integral Exponential Function

$\underset{3}{\overset{7}{\int }}{2}^{\left(9x\right)}\mathit{ dx}$

Step 1: Simplify and look for algebraic rewrites.

None in this example.

$\underset{3}{\overset{7}{\int }}{2}^{\left(9x\right)}\mathit{ dx}$

Step 2 Identify any term(s) that includes the base case $a^{\left(nx\right)}$.

Here you have 1 chunk, and it is the base case $a^{\left(nx\right)}$.

$\underset{3}{\overset{7}{\int }}{2}^{\left(9x\right)}\mathit{ dx}$

Step 3: Take the antiderivativeof the $a^{\left(nx\right)}$ special cases using their specific Recipe.

Chunk 1: $2^{\left(9x\right)}$

a = 2

n = 9

$\underset{3}{\overset{7}{\int }}{2}^{\left(9x\right)}\mathit{ dx}\mathit{=}{\frac{1}{\mathit{ln}\mathit{\left(}\mathit{2}\mathit{\right)}\mathit{\bullet }\mathit{9}}\mathit{\bullet }{2}^{\left(9x\right)}|}_{x=3}^{x=7}$

Step 4 ( Definite Integral ONLY ): Evaluate the antiderivative result using the Top – Bottom method.

$\underset{3}{\overset{7}{\int }}{2}^{\left(9x\right)}\mathit{ dx}\mathit{=}{\frac{1}{\mathbf{l}\mathbf{n}\left(\mathit{2}\right)\mathit{\bullet }\mathit{9}}\mathit{\bullet }{2}^{\left(9x\right)}|}_{x=3}^{x=7}$

$=\left({\frac{1}{\mathbf{l}\mathbf{n}\left(\mathit{2}\right)\mathit{\bullet }\mathit{9}}2}^{\left(9\left(7\right)\right)}\right)–\left({\frac{1}{\mathbf{l}\mathbf{n}\left(\mathit{2}\right)\mathit{\bullet }\mathit{9}}2}^{\left(9\left(3\right)\right)}\right)$

$\approx 1.478\times {10}^{18}$

Final Result Meaning: Remember the Definite Integral will always provide you a definite value , and the Indefinite Integral provides you a family of solutions .

The Net Area between the curve $f\left(x\right)=2^{\left(9x\right)}$ and the x-axis on the x-interval [ 3 , 7 ] is $1.478\times {10}^{18}$.

Since the final result is positive, you know without even seeing the graph that there is more area above the x-axis than below it.