Meaning: Limit Definition of the Derivative

We start by taking our traditional algebraic slope ( average rate of change) equation and rewrite it as what is called the Difference Quotient.

$y_2=\mathit{ f}\mathrm{(}x+h\mathrm{)}$       $y_1=\mathit{ f}\mathrm{(}x\mathrm{)}$

$y_2–y_1=\mathit{ f}\mathrm{(}x+h\mathrm{)}–\mathit{ f}\mathrm{(}x\mathrm{)}$

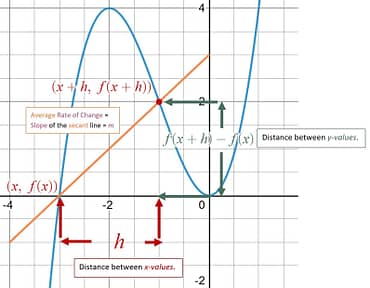
h is just another way to represent the distance between our x-values

$h=\mathrm{(}{\mathit{x}}_{\mathit{2}}\mathit{–}{\mathit{x}}_{\mathit{1}}\mathrm{)}$.

Here is the algebra they use to simplify it

$x_2\mathit{=}x+h\mathit{ }\mathit{ }{x}_1=\mathit{x}$

$x_2–x_1=(x+h)–x$

$x_2–x_1=h$

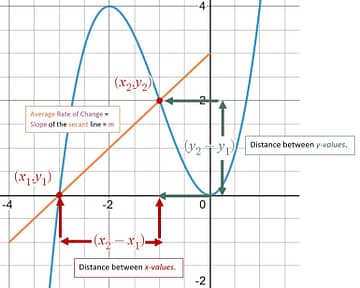
Slope = Difference Quotient = Average rate of change = Slope of the Secant Line = m

$\frac{y_2–y_1}{x_2–x_1}=\frac{f\mathrm{(}x+h\mathrm{)}–f\mathrm{(}x\mathrm{)}}{h}=m$  

Algebra

Slope = $\frac{y_2–y_1}{x_2–x_1}$

Calculus

Difference Quotient = $\frac{f\mathrm{(}x+h\mathrm{)}–f\mathrm{(}x\mathrm{)}}{h}$

The problem with the traditional algebraic method for finding slope is when we are trying to find the slope at a single point . At a single point , our x-values would be the same, which also means the distance between x-values ($h$)would be zero.

When you try to evaluate using algebra, both equations fail as we would get division by zero.

$x_1–x_1=0$

$h=0$

$\frac{y_2–y_1}{\overline{)x_1–x_1}}=\frac{f\mathrm{(}x+h\mathrm{)}–f\mathrm{(}x\mathrm{)}}{\overline{)h}}$

$\frac{y_2–y_1}{\overline{)0}}\mathit{=}\frac{f\mathrm{(}x+h\mathrm{)}–f\mathrm{(}x\mathrm{)}}{\overline{)0}}$

In comes calculus with the tool of a limit to solve the division by zero problem. Since a limit does not care if we actually get there or not, it only cares what it looks like we are heading towards. So, we can see what it looks like when we are heading towards as the distance between our x-values go to zero, a single point.

We apply the limit $\mathrm{(}\underset{\mathit{h}\mathbf{\to }\mathbf{0}}{\lim }\mathrm{)}$to the Difference Quotient, and we have the ability now to find the slope ( instantaneous rate of change) at a single point.

The limit statement is showing us what is happening to this equation as the distance between our x-values ($\mathit{h}$) heads to 0.

This is called the Slope of the Tangent Line (a line that touches at just one point, $\mathrm{(}x,f\left(x\right)\mathrm{)}$), and that slope will change depending upon the x-value we are evaluating at because the tangent point changes and therefore the tangent line changes, and the slope of that line changes.

 Calculus Slope = Instantaneous rate of change = Slope of the Tangent Line = m

$f^{\prime }\mathrm{(}x\mathrm{)}=\underset{\mathit{h}\mathbf{\to }\mathbf{0}}{\lim }\frac{f\mathrm{(}x+h\mathrm{)}–f\mathrm{(}x\mathrm{)}}{h}=m$

Remember: The derivative,${\mathit{f}}^{\mathit{\prime }}\mathrm{(}\mathit{x}\mathrm{)}$ , is an equation for finding the slope , m ,at a single point, a single instance in time.

Just like the slope formula,$\mathit{ }\frac{{\mathit{y}}_{\mathit{2}}\mathit{–}{\mathit{y}}_{\mathit{1}}}{{\mathit{x}}_{\mathit{2}}\mathit{–}{\mathit{x}}_{\mathit{1}}}$, is an equation for finding the slope , m ,between two points.