Riemann Sums Using Trapezoids

While the majority of Riemann Sum problems that you encounter will be based upon finding the areas of rectangles , the other geometric shape that you will commonly be asked to use to estimate the area between a curve and the x-axis is a trapezoid . The main idea behind what you are doing remains the same with this method. You are still using the area of a shape to estimate the area between a curve and the x-axis . The main difference comes down to the area formula you use for each subinterval. Since you are now using trapezoids as our shape, you need to now use the area of a trapezoid formula.

$A=\frac{1}{2}\left(\mathit{base }1+\mathit{base }2\right)\bullet \mathit{height}$

$A=\frac{1}{2}\left(b_1+b_2\right)\bullet h$

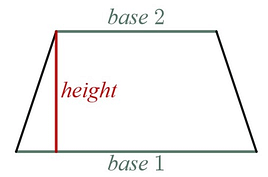
Where I think most people get confused when using trapezoids is that you are not using the trapezoid shape in the standard orientation like you see in the image above. When using trapezoids to estimate the area between a curve and the x-axis , you actually rotate the trapezoids ${90}^{°}$clockwise (like you see in the image below) to get your areas for each subinterval. The formula for finding the area of the trapezoid does not change, and the labeling of the pieces (i.e., bases and height) of the trapezoid does not change, but it will take your brain a minute to catch up to what is happening with the new orientation.

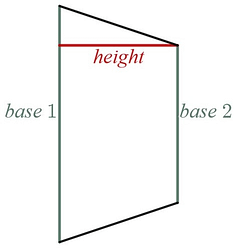
Putting this in the context of a real graph that you are trying to estimate the area between the curve and the x-axis of, you see that the labels of the trapezoid are fighting how your brains want to think about those terms base and height . The bases are actually going up and down they are the function values, $f\left(x_i\right)$, and the height are the width of the subintervals , $∆x$.

$A=\frac{1}{2}\left(\mathit{base }1+\mathit{base }2\right)\bullet \mathit{height}$                                          $A=\frac{1}{2}\left(b_1+b_2\right)\bullet h$

$A=\frac{1}{2}\left(b_1+b_2\right)\bullet h$                                                                  $A=\frac{1}{2}\left(f\left(x_i\right)+f\left(x_{i+1}\right)\right)\bullet ∆x$

The big difference between the rectangle method and the trapezoid method is that you will need to calculate 2 y-values, $f\left(x_i\right)\mathit{ and }f\left(x_{i+1}\right)$, for each of your trapezoids to get your base 1 and base 2 values. The height for each trapezoid will come from the $∆x$ or the width of the given subintervals if you are using a table of values.

$A_n=\frac{1}{2}\left(\mathit{base }1+\mathit{base }2\right)\bullet \mathit{height}$

$A_n=\frac{1}{2}\left(b_1+b_2\right)\bullet h$

$A_n=\frac{1}{2}\left(f\left(x_i\right)+f\left(x_{i+1}\right)\right)\bullet ∆x$