Riemann Sums Using Rectangles

Unit 5: Riemann Sums Riemann Sums Using Rectangles

Riemann Sums have you estimate the area between a curve and the x-axis using the areas of standard geometric shapes. The most common shape used to estimate the area is a rectangle. You will be using the areas of rectangles to estimate the area between a curve and the x-axis . Here is how you go from the area of a rectangle formula you know, and turn it into the formula you will use for Riemann Sums.

You start with your standard area of a rectangle formula.		$Area = base ∙ height$ $A = b ∙ h$
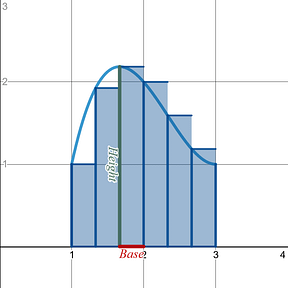
You then take that standard area of a rectangle formula and apply it to an actual curve, $f (x)$ . The base of your rectangle is the distance between x-values , which is called $∆ x$ , or the change in x . The height of your rectangles will be the y-values you get by plugging in a specific x-value . The notation for that looks like $f (x_{i})$ . Where the input, $x_{i}$ , is what changes the height of each rectangle. Those inputs , x-values , will be *the key* to determining the height of each of your rectangles .		$Area = base ∙ height$ $A = b ∙ h$ $A = ∆ x ∙ f (x_{i})$
You will be given directions on: i) How to break your overall x-interval , [ a , b ], into the smaller subintervals , $∆ x$ , that you will use as the $base = ∆ x$ . The $∆ x$ is often the same value from rectangle to rectangle, but you will see AP Calc Exam questions that only provide you a table of values , and that table of values may not have a consistent $∆ x$ . Be careful when using a table.
ii) How to select the evaluation point, $x_{i}$ , you will use to find your $height = f (x_{i})$ . The five most common methods for selecting the evaluation point are the Left Hand Sum, Right Hand Sum, Midpoint Sum, Upper Sum, and Lower Sum.
Left Hand Sum	Right Hand Sum	Midpoint Sum	Upper Sum	Lower Sum
The evaluation points, $x_{i}$ , are the left hand endpoint of your subintervals .	The evaluation points, $x_{i}$ , are the right hand endpoints of your subintervals .	The evaluation points, $x_{i}$ , are the midpoint of your subintervals .	The upper sum requires you to make the decision for the evaluation point, $x_{i}$ . You must choose either the left or right endpoint of the x-subinterval as your $x_{i}$ based on which one gives the largest y-value .	The lower sum requires you to make the decision for the evaluation point, $x_{i}$ . You must choose either the left or right endpoint of the x-subinterval as your $x_{i}$ based on which one gives the smallest y-value .

The Summation Portion: Once you have calculated the area of the rectangle for each of your subintervals, you then add up all those areas to get the *net* area between a curve and the x-axis . *Net* area means you treat area above the x-axis as positive and area below the x-axis as negative, and then add them all up. A positive net area does not tell you that all the area is above the x-axis only that there is more area above the x-axis than area below the x-axis . A negative net area does not tell you that all the area is below the x-axis only that there is more area below the x-axis than area above the x-axis . A zero net area does not tell you that there is no area between the curve and the x-axis , only that there is equal amounts of area above and below the x-axis .
Meaning: In terms of an actual application (word) problem your result will be the *net* total amount of whatever the units on the top part of your rate. In terms of $\frac{dy}{dx}$ , it would be the *net* total of the $dy$ units. If the rate’s unit is $\frac{m}{s}$ , the result would be the *net* total meters traveled from the starting point (displacement) on the x-interval you were given, [ a , b ]. If your rate’s unit is talking fish per day, $\frac{fish}{day}$ , then the result would be the *net* total fish accumulated during the x-interval you were given, [ a , b ].