Method 1: Given a Slope Field
When you are given a slope field graph (graph with a bunch of little lines), you are given a physical representation of the SLOPE at those given points based on a given differential equation. This is basically the graph of answers. When you look at the graph it really is the same type of process as you learned when you learned how to read the 1 st Derivative off of a given f(x) graph. Which means we are back to looking at this in terms of increasing means positive slopes, decreasing means negative slopes, and horizontal means a zero slope. It is the derivative triangle coming back.

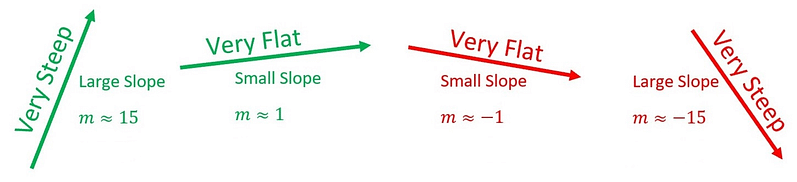
You also have to keep in mind what the steepness of the slope means.
When you are given the actual slope field graph to start the problem, they generally want you to identify which of a list of given differential equations, matches your given slope field graph.
Step 1: Choose a point, ( x , y ), that has a slope that is horizontal.
Just like when you were learning to graph the derivative based on the original function, the easiest point to identify is a point where the tangent line is horizontal. When the tangent line is horizontal then you know with 100% certainty that the value of the slope at that point is zero. This tells you that the value of your differential equation at that point is also zero, .
Step 2: Plug the point, ( x , y ), you selected in Step 1 into the options you were given for possible differential equation answers.
If from that list you are able to narrow it down to just one differential equation that gives you zero as its answer, great you are done and that is your answer.
If you are only able to eliminate a few, but not all of the differential equations, then you should repeat these same two steps starting with Step 1 . Choose another point that has a horizontalslope. This new point will have a different value for either x or y , and that means it should provide you another opportunity to narrow down the list of possible solutions for your differential equation.
Step 3 (only if horizontal lines don’t work) : Choose a point, ( x , y ), that has a vertical slope line.
Vertical slope lines occur when your differential equation has division by zero occurring. These are usually the places the original equation has a vertical asymptote , but could also just be where you have a vertical tangent line .
Step 4 (only if horizontal lines don’t work) : Plug the point, ( x , y ), you selected in Step 3 into the options you were given for possible differential equation answers.
Narrow down your options from the list of differential equations to the ones that would give you division by zero if you plugged in the point you chose in Step 3. If you are not able to narrow it down to one answer, repeat the process of Step 3 and Step 4 with another point that has a vertical tangent line .
Step 5 (only if horizontal and vertical lines don’t work) : Choose a point, ( x , y ), that has a slope you feel confident you have a good idea of its approximate value.

Step 6 (only if horizontal and vertical lines don’t work) : Plug the point, ( x , y ), you selected in Step 5 into the options you were given for possible differential equation answers.
Narrow down your options from the list of differential equations to the ones that would give you a slope that matches the slope line drawn at that specific point on the slope field graph. Repeat Step 5 and Step 6 until you have narrowed it down to your final answer.

