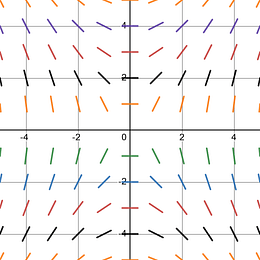
Example 1: Given a Slope Field

Shown above is a slope field for which of the following differential equations?

A)  $\frac{\mathit{dy}}{\mathit{dx}}=\frac{2x}{y}$

B)  $\frac{\mathit{dy}}{\mathit{dx}}=\frac{2y}{x}$

C)  $\frac{\mathit{dy}}{\mathit{dx}}=2x+y$

D)  $\frac{\mathit{dy}}{\mathit{dx}}={(y+1)}^2$

Identifier: The question itself uses the term “slope field” and you are given a graph that has a slope field drawn on it.

Step 1: Choose a point, ( x , y ), that has a slope that is horizontal.

In this example you could choose any ( x , y ) along the y-axis since all the slope lines on the y-axis are horizontal.

For this example, I have chosen the point (0,2).

Horizontal at (0,2)

Step 2: Plug the point, ( x , y ), you selected in Step 1 into the options you were given for possible differential equation answers.

Once you plug the point you chosen in Step 1, (0,2), you will see that the only answer that matches a horizontal slope, zero slope, is answer (A).

Chosen Point: (0,2)

A)  $\frac{\mathit{dy}}{\mathit{dx}}=\frac{2x}{y}$

$\frac{\mathit{dy}}{\mathit{dx}}=\frac{2\left(0\right)}{\left(2\right)}=0$

B)  $\frac{\mathit{dy}}{\mathit{dx}}=\frac{2y}{x}$

$\frac{\mathit{dy}}{\mathit{dx}}=\frac{2\left(2\right)}{\left(0\right)}=\mathit{Does\; Not\; Exist}$

C)  $\frac{\mathit{dy}}{\mathit{dx}}=2x+y$

$\frac{\mathit{dy}}{\mathit{dx}}=2\left(0\right)+\left(2\right)=2$

D)  $\frac{\mathit{dy}}{\mathit{dx}}={(y+1)}^2$

$\frac{\mathit{dy}}{\mathit{dx}}={\left(\right(2)+1)}^2=9$

Final Result:

The differential equation that matches the results of the given slope field is answer (A).