Example 1: Related Rates

A 25ft long ladder leans against a vertical wall. If the lower end is being moved away from the wall at a rate of $6\frac{\mathit{ft}}{s}$, how fast is the height of the top changing when the lower end of the ladder is 7ft from the base of the wall.

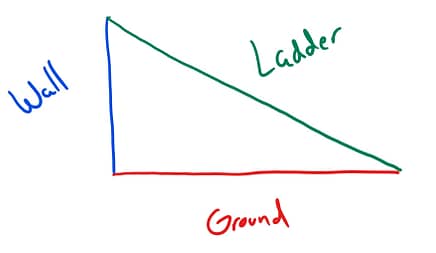
Step 1: Read through the problem once, and sketch out a diagram of what is happening.

In this example we have a ladder leaning against a wall. Our picture would look something like this, a right triangle.

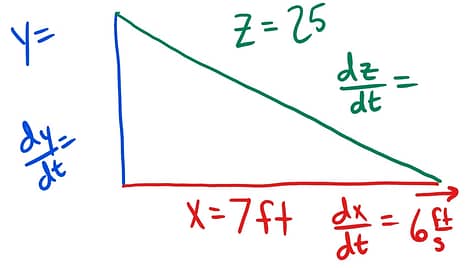
Step 2: Read through the problem a second time, identify all the given and implied material, and where it is located on you diagram.

The first thing I do on a problem like this is immediately label the sides of the triangles with a flat piece ( x , y , z ) and a rate of change piece $\left(\frac{\mathit{dx}}{\mathit{dt}}, \frac{\mathit{dy}}{\mathit{dt}},\frac{\mathit{dz}}{\mathit{dt}}\right)$. I do this for a couple of reasons.

1)      This right triangle setup is a very common setup for these types of problems. It might not always be a ladder and a wall in the problems, but the picture I draw in Step 1 is always a right triangle. Since I have tried many different types of related rates problems, I know this is a common method used to solve those problems.

2)      I know that I need a flat piece and a rate of change piece for each side of this triangle. Again, this is common, but also because this is the way many right triangle related rates problems go.

Label the given information:

1)      “A 25ft long ladder leans against a vertical wall.” This is a flat amount not a rate of change, and it is describing the length of the ladder so I label z = 25ft .

2)      “lower end is being moved away from the wall at a rate of $6\frac{\mathit{ft}}{s},“$ We see the word rate and the units, feet per second, and we know we are looking at a rate of change piece that is telling us how the bottom of the ladder is moving, which effects how the ground (x-side) of our picture is changing. I label $\frac{\mathit{dx}}{\mathit{dt}}=6$, and it would be positive because it is an increasing amount.

3)      “lower end of the ladder is 7ft from the base of the wall.” Remember that a related rate problem is just a snapshot of a point in time, and at the point in time in this problem the distance along the bottom of our triangle would be a flat 7ft . I label the bottom x = 7 .

4)       

Label the implied information:

The more of these you do, the more easily you will be able to pick out those implied pieces.

1)      When you think about what is happening to the ladder in this process, as the ladder falls it never changes from being a 25ft long ladder. This tells us the rate of change along the ladder would be zero. I label  $\frac{\mathit{dz}}{\mathit{dt}}=0$. Keep an eye out on a triangle problem for a side that has no change.

2)      If you have 2 out of 3 sides of a right triangle, you can use your good old friend the Pythagorean Theorem, $a^2+b^2=c^2$, to find that 3 ^rd side. For this problem, $x^2+y^2=z^2$. We use that to find the value for y, and label y = 24 .

Label the Given Information:

Label the Implied Information:

Pythagorean Theorem:

$x^2+y^2=z^2$

${\left(7\right)}^2+y^2={\left(25\right)}^2$

$49+y^2=625$

$y^2=625–49$

$y^2=576$

$y=\sqrt{576}$

$y=24$

Step 3: Identify the rate of change you are being asked to find.

Here we are being asked to find, “how fast is the height of the top changing,”? Which tells us we want to know how the y-side of our triangle is changing, which is $\frac{\mathit{dy}}{\mathit{dt}}$.

Step 4: Find an equation that relates the flat amounts to each other.

This can sometimes be the equation you used to find one of your missing pieces.

In this example we know we can relate all the sides (flat pieces) of a right triangle using Pythagorean Theorem, which means this will be the equation we want to use.

$x^2+y^2=z^2$

$x^2+y^2=z^2$

Step 5: Take the derivative of the equation using implicit differentiation.

You will more times than not be $\frac{d}{dt}$-ing the equation, or taking the derivative with respect to time. Most word problems work with time.

We will $\frac{d}{dt}$ our Pythagorean Theorem using implicit differentiation. Remembering that every time I take a derivative, I get extra stuff. Here our extra stuff will take the form $\frac{d\overline{)}}{dt}$. Filling our box in with the letter of whatever we took the derivative of.

$x^2+y^2=z^2$

$\frac{d}{dt}\left(x^2+y^2=z^2\right)$

1)      $x^2$: Power Rule

Derivative: $2x\frac{d\overline{)x}}{dt}$

2)      $y^2$: Power Rule

Derivative: $2y\frac{d\overline{)y}}{dt}$

3)      $z^2$: Power Rule

Derivative: $2z\frac{d\overline{)z}}{dt}$

Overall Derivative Result: $2x\frac{\mathit{dx}}{\mathit{dt}}+2y\frac{\mathit{dy}}{\mathit{dt}}=2z\frac{\mathit{dz}}{\mathit{dt}}$

Step 6: Plug in all of the pieces you have identified in Step 2 into the derivative equation you just created, and solve for the piece you need.

1)      $x=7$

2)      $\frac{\mathit{dx}}{\mathit{dt}}=6$

3)      $y=24$

4)      $z=25$

5)      $\frac{\mathit{dz}}{\mathit{dt}}=0$

6)      $\frac{\mathit{dy}}{\mathit{dt}}=?$

Once I have plugged in all my values, I can see that the only piece left missing is $\frac{\mathit{dy}}{\mathit{dt}}$, which is what I am being asked to find. Solve to find $\frac{\mathit{dy}}{\mathit{dt}}$.

If you have a piece other than what you are trying to find left as a variable in your equation, then you have to start trying to find other implied values from the problem in order to plug in for all the values except the ONE value you are trying to find.

$2x\frac{\mathit{dx}}{\mathit{dt}}+2y\frac{\mathit{dy}}{\mathit{dt}}=2z\frac{\mathit{dz}}{\mathit{dt}}$

$2\left(7\right)\left(6\right)+2\left(24\right)\frac{\mathit{dy}}{\mathit{dt}}=2\left(25\right)\left(0\right)$

$84+48\frac{\mathit{dy}}{\mathit{dt}}=0$

$\begin{array}{c}84\\ –84\end{array}+48\frac{\mathit{dy}}{\mathit{dt}}=\begin{array}{c}0\\ –84\end{array}$

$48\frac{\mathit{dy}}{\mathit{dt}}=–84$

$\frac{48\frac{\mathit{dy}}{\mathit{dt}}}{48}=\frac{–84}{48}$

$\frac{\mathit{dy}}{\mathit{dt}}=–\frac{7}{4}$

Final Result:

The final result is that the height of the top of the ladder is changing at $–\frac{7}{4}\frac{\mathit{ft}}{s}$. Don’t forget your units.

The negative is correct and tells us that the ladder is moving down.

$\frac{\mathit{dy}}{\mathit{dt}}=–\frac{7}{4}$