Example 7: 2 Different Horizontal Asymptotes (Pro Level)

Find all horizontal asymptotes of $f\left(x\right)=\frac{3x–2}{\sqrt{4x^2+5}}$.

Step 1: Determine if you are being asked to find a single limit, $\underset{x\to \mathrm{\infty }}{\lim }$ or $\underset{x\to –\mathrm{\infty }}{\lim }$, or if you are being asked to find the horizontal asymptotes of an equation, which means you have to do both limits no matter what.

Here we are being asked to find the horizontal asymptotes of the equation. This means we must consider what is happening in both directions, x approaches negative infinity, $x\to –\infty$, and as x approaches infinity, $x\to \infty$.

$\underset{x\to –\infty }{\lim }\frac{3x–2}{\sqrt{4x^2+5}}$

$\underset{x\to \mathrm{\infty }}{\lim }\frac{3x–2}{\sqrt{4x^2+5}}$

Step 2: Determine the single leading behavior (dominant term) over your entire equation. It may show up in multiple places in the equation.

When you have a root in an equation it is important to remember that powers inside a root are going to look different than powers outside the root, but they may have the same level of dominance.

For example, $\sqrt{x^2}=\pm \mathit{x\; or }\sqrt{x^6}=\pm$.

So, you will want to identify the dominant term inside the root, identify the dominant term outside the root, and then compare those to determine the overall dominant term.

In our example, outside the root the dominant term is $x$, inside the root the dominant term is $x^2$.

If you compare those you will see that they are actually the same level of dominance.

$\sqrt{x^2}=\pm x$

Do not forget that you have to consider $\pm x$ because we are squaring the term inside the square root.

$\underset{x\to –\infty }{\lim }\frac{\overline{)x}–2}{\sqrt{4\overline{)x^2}+5}}$

$\underset{x\to \mathrm{\infty }}{\lim }\frac{\overline{)x}–2}{\sqrt{4\overline{)x^2}+5}}$

Step 3: Divide every term in the equation by the dominant term, and simplify all the fractions you have just created.

This is where the next “pro” level move comes in.

As you head to $–\mathrm{\infty }$, you will need to divide outside the root by $–x$, since the x-values would be negative in that direction. Inside the root you will divide by $x^2 \mathrm{s}$ince

${(–x)}^2=x^2$.

As you head to $\mathbf{+}\mathrm{\infty }$, you will need to divide by$\mathbf{+}x$, since the x-values would be positive in that direction. Inside the root you will divide by $x^2 \mathrm{s}$ince

${(\mathbf{+}x)}^2=x^2$.

You then simplify those new fractions by canceling the x ’s.

$\underset{x\to –\infty }{\lim }\frac{\frac{3x}{–x}–\frac{2}{–x}}{\sqrt{\frac{4x^2}{x^2}+\frac{5}{x^2}}}=\underset{x\to –\infty }{\lim }\frac{–3–\frac{2}{–x}}{\sqrt{4+\frac{5}{x^2}}}$

$\underset{x\to \infty }{\lim }\frac{\frac{3x}{x}–\frac{2}{x}}{\sqrt{\frac{4x^2}{x^2}+\frac{5}{x^2}}}=\underset{x\to \infty }{\lim }\frac{3–\frac{2}{x}}{\sqrt{4+\frac{5}{x^2}}}$

Step 4: Apply a limit identity that you are given to each simplified term in your equation.

$\underset{x\to \infty }{\lim }\frac{1}{x}=0$

We will apply this limit identity to three different terms in each equation, $\frac{2}{–x}$, $\frac{5}{x^2}$,and $\frac{2}{x}$. All three are heading to zero.

$\underset{x\to –\infty }{\lim }\frac{–3–\overline{)\frac{2}{–x}}}{\sqrt{4+\overline{)\frac{5}{x^2}}}}=\frac{\overline{)–3}+\overline{)0}}{\sqrt{\overline{)4}+\overline{)0}}}=\frac{–3}{\sqrt{4}}=\frac{–3}{2}$

$\underset{x\to \infty }{\lim }\frac{3–\overline{)\frac{2}{x}}}{\sqrt{4+\overline{)\frac{5}{x^2}}}}=\frac{\overline{)3}+\overline{)0}}{\sqrt{\overline{)4}+\overline{)0}}}=\frac{3}{\sqrt{4}}=\frac{3}{2}$

Step 5: Draw your final conclusion about your limits based upon the Step 4 simplification, and give your final answer.

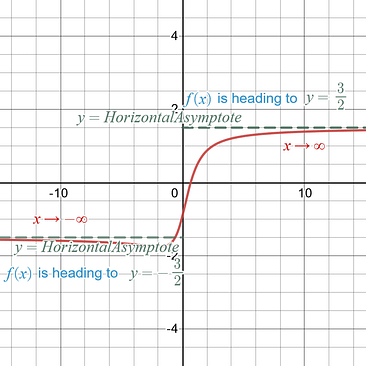
Here we have two different results.

As the x-values head to $–\mathrm{\infty }$, the equation’s y-values head to $–\frac{\mathbf{3}}{\mathbf{2}}$.

As the x-values head to $\mathrm{\infty }$, the equation’s y-values head to $\frac{\mathbf{3}}{\mathbf{2}}$.

$\underset{x\to –\infty }{\lim }\frac{3x–2}{\sqrt{4x^2+5}}=\frac{–3}{2}$

$\underset{x\to \mathrm{\infty }}{\lim }\frac{3x–2}{\sqrt{4x^2+5}}=\frac{3}{2}$

Final Result:

The function, $f\left(x\right)=\frac{3x–2}{\sqrt{4x^2+5}}$, has two horizontal asymptotes.

A horizontal asymptote as x approaches negative infinity, $x\to –\infty$, the function heads to $y=–\frac{\mathbf{3}}{\mathbf{2}}$.

A horizontal asymptote as x approaches infinity, $x\to \infty$, the function heads to $y=\frac{\mathbf{3}}{\mathbf{2}}$.